Euler Angles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
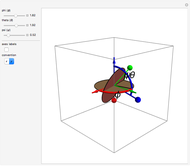
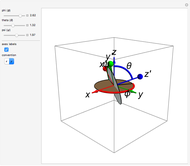
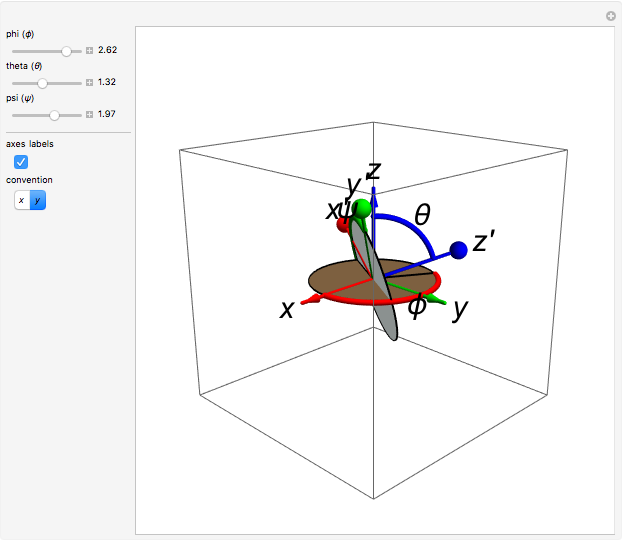
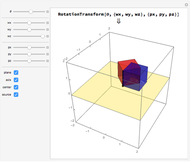
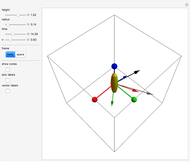
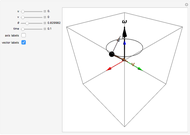
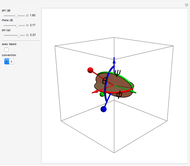
The Euler angles are a classical way to specify the orientation of an object in space with respect to a fixed set of coordinate axes. This Demonstration shows two of the several implementations of the Euler angles 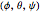 . The initial
. The initial 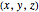 axes are indicated by the red, green, and blue arrows, while the final
axes are indicated by the red, green, and blue arrows, while the final 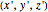 axes are indicated by the red, green, and blue spheres.
axes are indicated by the red, green, and blue spheres.
Contributed by: Frederick W. Strauch (August 2011)
Open content licensed under CC BY-NC-SA
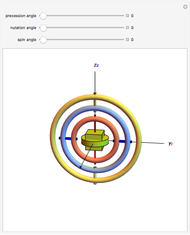
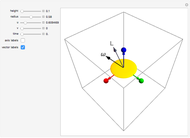
Snapshots
Details
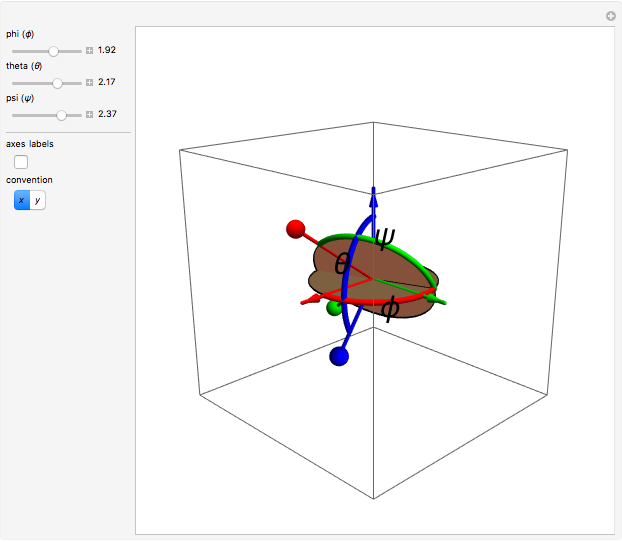
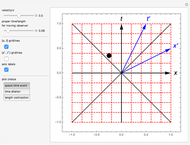
The Euler angles 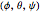 are used to define a sequence of three rotations
are used to define a sequence of three rotations 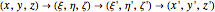 , by the angles
, by the angles 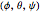 about the
about the  ,
,  , or
, or  , and
, and 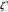 axes, respectively. If the second rotation is about the
axes, respectively. If the second rotation is about the  axis, this is called the "
axis, this is called the " convention". The net transformation is given by the matrix equation
convention". The net transformation is given by the matrix equation
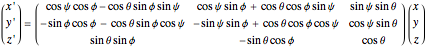 .
.
This convention is used by Thornton and Marion [1] in Chapter 11.
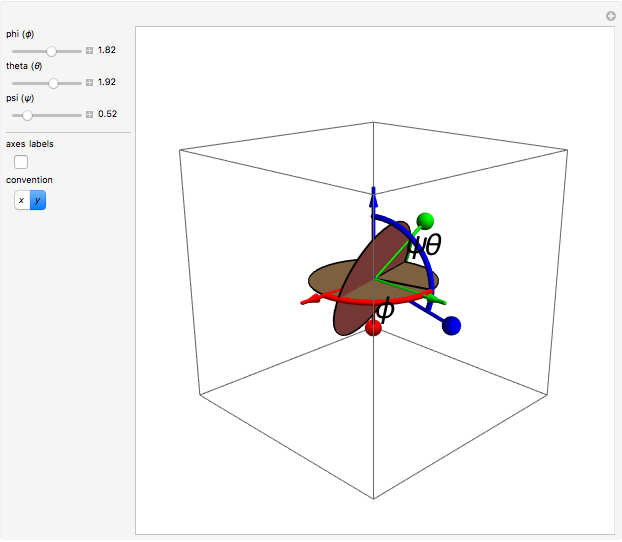
If the second rotation is about the  axis, this is called the "
axis, this is called the "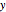 convention". The net transformation is given by the matrix equation
convention". The net transformation is given by the matrix equation
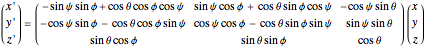 .
.
This convention is used by J. R. Taylor [2] in Chapter 10.
Both conventions are described by H. Goldstein [3] in Chapter 4.
See also Euler angles.
References
[1] S. T. Thornton and J. B. Marion, Classical Dynamics of Particles and Systems, Belmont, CA: Brooks/Cole, 2004.
[2] J. R. Taylor, Classical Mechanics, Mill Valley, CA: University Science Books, 2005.
[3] H. Goldstein, Classical Mechanics, Reading, MA: Addison-Wesley, 1980.
Permanent Citation