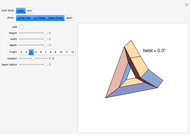
Euler's Rotation Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
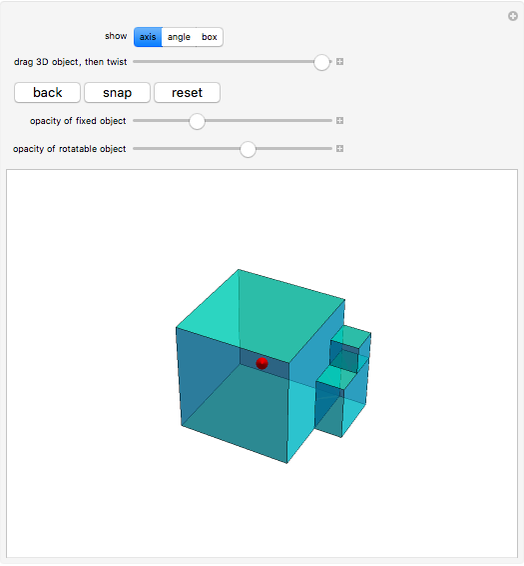
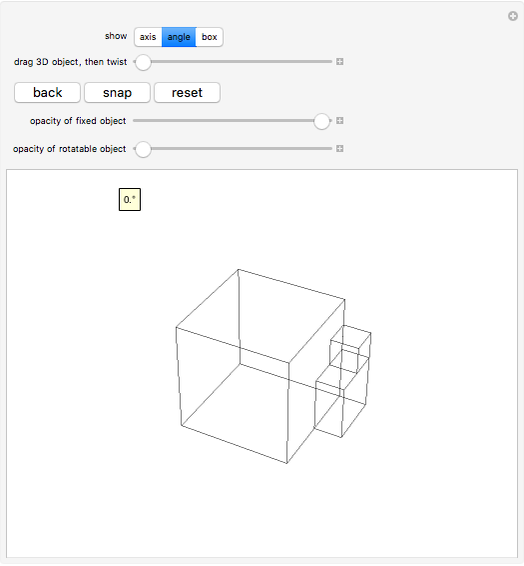
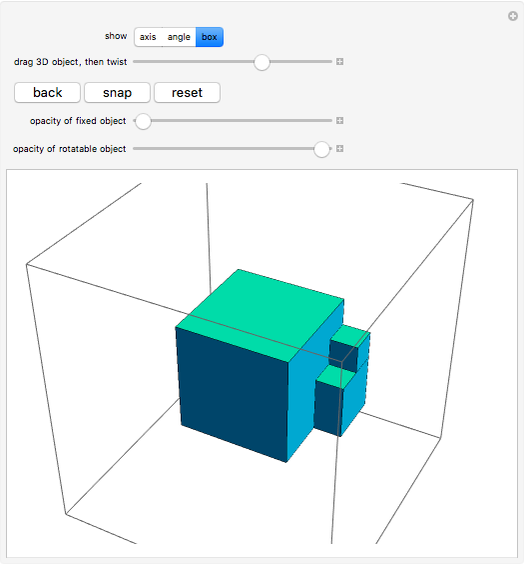
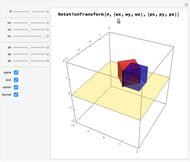
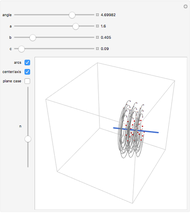
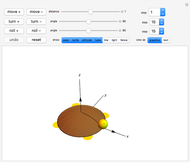
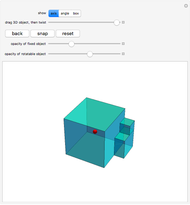
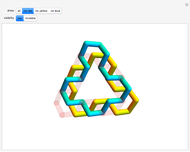
Drag the 3D graphic; then you can use the "drag... twist" control. No matter how an object changes position about its center, it can always be brought back to its original position with a single rotation. This Demonstration reveals the required rotation angle and rotation axis.
Contributed by: Tom Verhoeff (Eindhoven University of Technology) (November 2014)
Open content licensed under CC BY-NC-SA
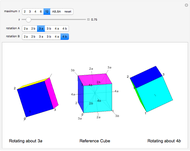
Snapshots
Details
The "show" control lets you toggle the angle, axis, and viewing box. The "drag... twist" slider controls the angular position of an intermediate copy as it rotates back to the original. The "back" button puts the object back into its original position. The "snap" button moves the original to the currently rotated position. The "reset" button resets the configuration to the initial state.
Euler's rotation theorem states that every 3D motion that keeps (at least) one point fixed is a rotation. For more detail, see [1]. Suppose the object  is rotated about the axis
is rotated about the axis 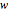 through an angle
through an angle  . This Demonstration defines the inverse operation that, given the attitudes of two objects with a common center, returns the angle
. This Demonstration defines the inverse operation that, given the attitudes of two objects with a common center, returns the angle  and axis
and axis 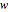 such that the second attitude is obtained from the first by rotating the latter about axis
such that the second attitude is obtained from the first by rotating the latter about axis 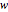 over angle
over angle  .
.
This Demonstration also illustrates how to use the dynamically updated ViewPoint and ViewVertical in order to show the original object in a fixed position, while you drag the object.
Reference
[1] Wikipedia. "Euler's Rotation Theorem." (Nov 14, 2014) en.wikipedia.org/wiki/Euler's_rotation _theorem.
Permanent Citation
"Euler's Rotation Theorem"
http://demonstrations.wolfram.com/EulersRotationTheorem/
Wolfram Demonstrations Project
Published: November 17 2014