Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Understanding Special Relativity: The Lorentz Transformation, Time Dilation, and Length Contraction

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

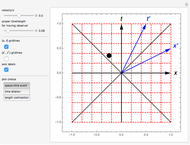
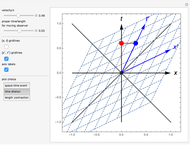
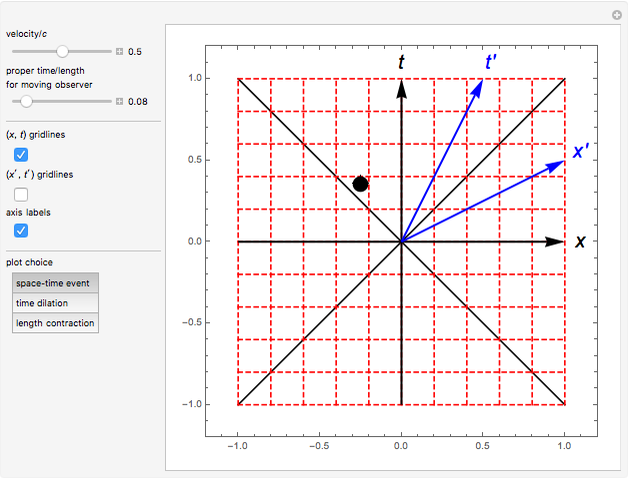
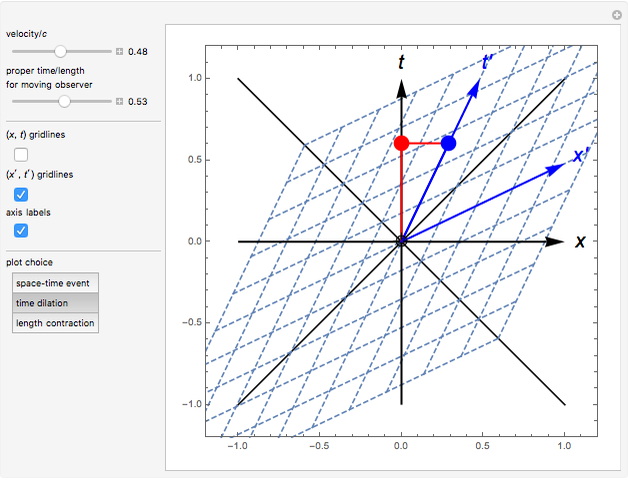
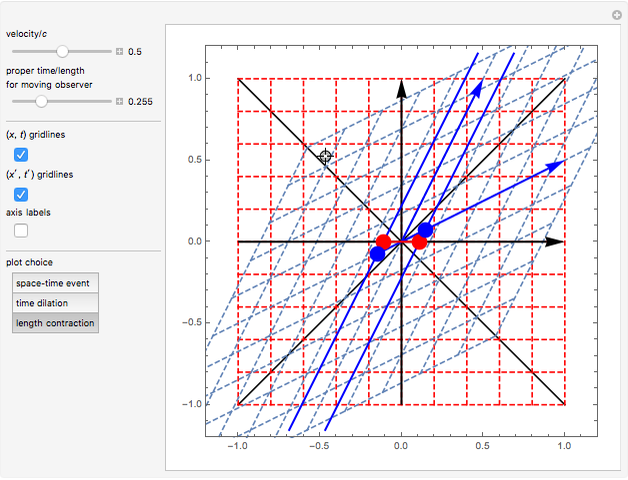
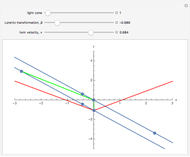
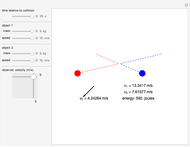
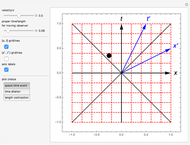
The Lorentz transformation describes how two observers in relative motion can relate their measurements of space and time. This Demonstration illustrates the space and time axes for two observers, one at rest (black axes, red gridlines) and one in motion (blue axes and gridlines) for a single space-time event, time dilation, or length contraction. The coordinate axes can be shown for each observer, and the relative velocity can be changed at will.

[more]

You can drag the space-time event (black dot) and see its and coordinates by mousing over it.

Time dilation is the phenomenon whereby two observers disagree on the time interval between two events: moving clocks run slowly. Here the proper time of a moving observer (in blue) corresponds to a longer (dilated) time for an observer at rest (in red). You can change the proper time.

Length contraction (also known as Lorentz–FitzGerald contraction) is the phenomenon whereby two observers disagree about the length of an object: moving objects shrink. Here the proper length of a moving object (worldlines in blue) corresponds to a shorter (contracted) length for an observer at rest (in red). You can change the proper length.

[less]

Contributed by: Frederick W. Strauch (August 2011)
Open content licensed under CC BY-NC-SA

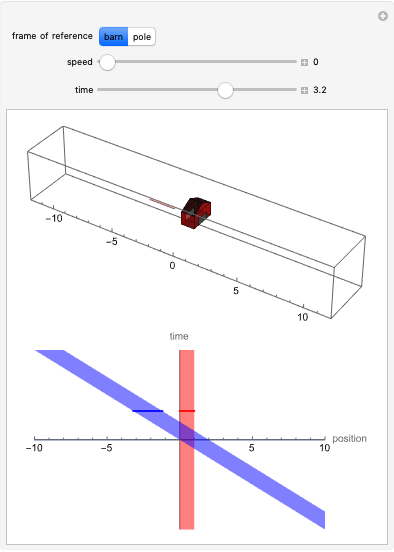
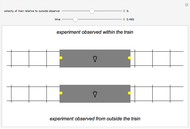
Snapshots

Details

The Lorentz transformation between two reference frames with coordinates and , in relative motion with velocity , can be represented by 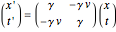, or the inverse 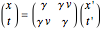, where 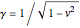and . The inverse transformation is used to plot gridlines of constant and .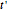

See also:

http://en.wikipedia.org/wiki/Lorentz_transformation

http://en.wikipedia.org/wiki/Time_dilation

http://en.wikipedia.org/wiki/Length_contraction

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send