Filtering Images in the Frequency Domain

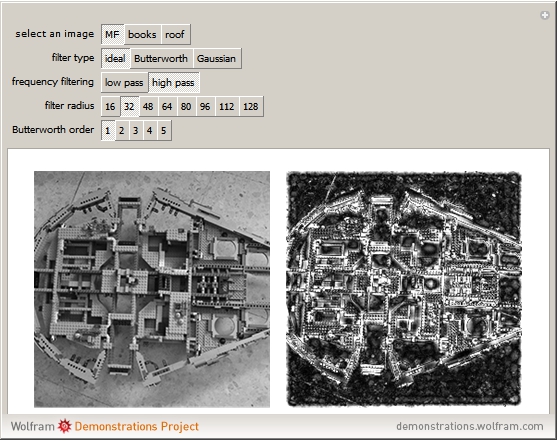
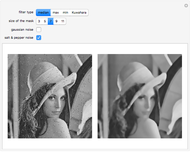
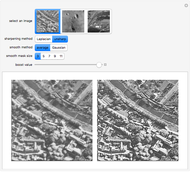
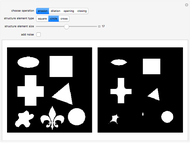
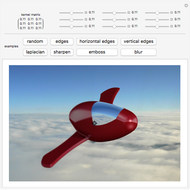
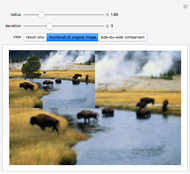
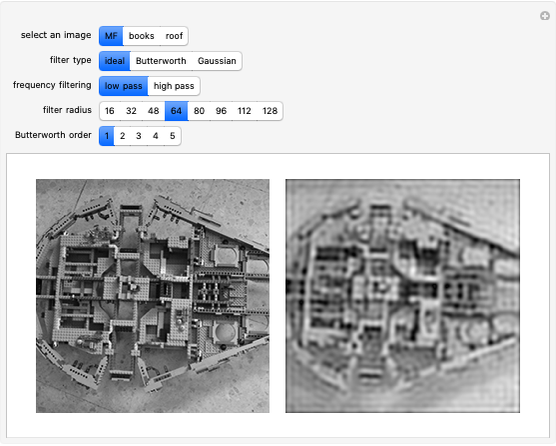
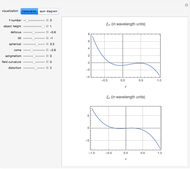
This Demonstration shows the effect of filtering images in the frequency domain. Low-pass and high-pass filtering of images are obtained when applying different filters. Filtering images can be done in the spatial domain by convolving a mask (or kernel) of different sizes with the image. However, the convolution operation is multiplication in the frequency domain, which eases filtering in the Fourier domain. Three basic filters can be defined for filtering an image to allow passing high or low spatial frequencies. Low-pass filtering produces smoothing, while high-pass filtering gives images that highlight the transitions of gray levels, which are the edges. The filters are the ideal, Butterworth, and Gaussian filters.