Surfaces of Wave Normals in Crystals

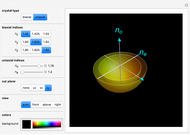
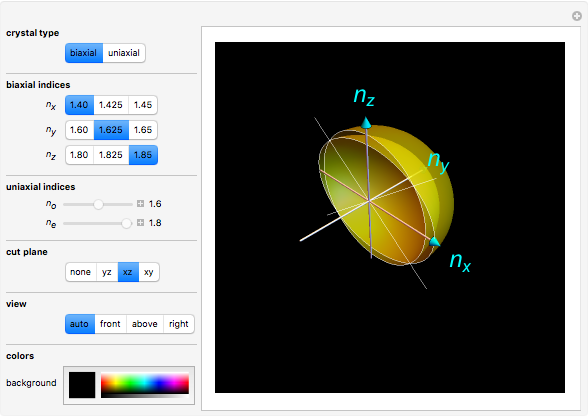
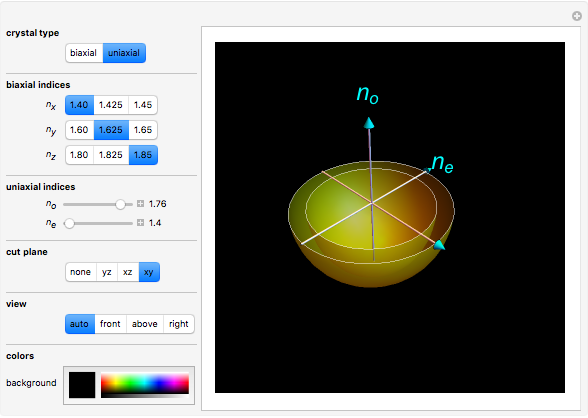
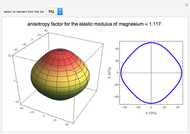
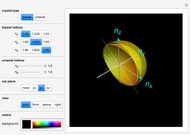
The surfaces of wave normals in crystals (Fresnel's equation of wave normals) are the solutions for the wavenumber of a monochromatic plane wave propagating inside an optical anisotropic material (crystal). This material is characterized by a dielectric permittivity tensor. Application of Maxwell's equations tells us that it is possible that two waves could propagate in the crystal, thus producing two wavenumbers obtained from the intersection of the wave propagation direction with the wave normal surfaces. When only one solution is obtained (one intersection), only one wave propagates and the direction is defined as the optical axis.