Finding Roots Using Binary or Interpolation Search


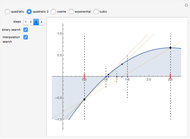
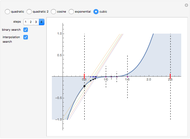
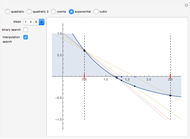
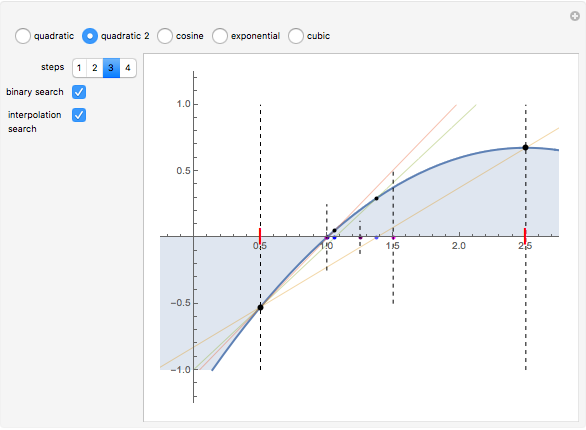
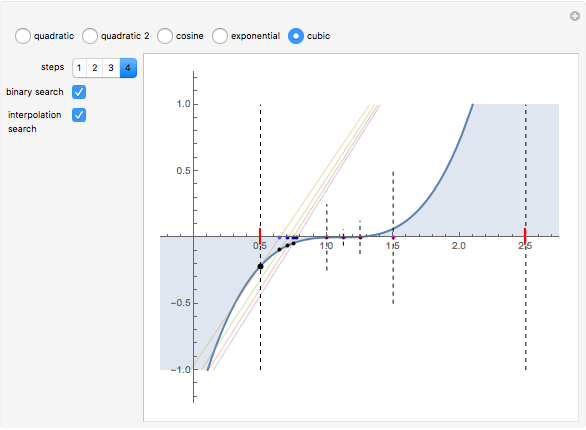
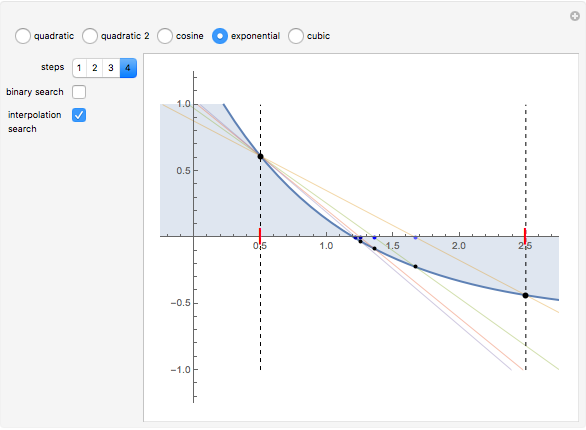
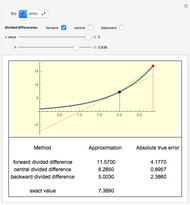
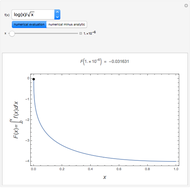
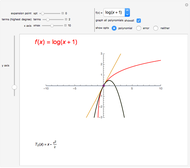
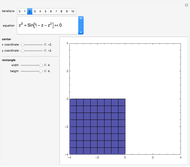
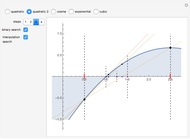
	A binary search algorithm is often used to search for a certain element in a sorted sequence. It can also be used to find a point where a function is zero (if the function is monotonic over the interval, there is one such point). Instead of dividing the interval, an interpolating search (the secant method) uses linear interpolation to guess where the root might be. This method usually converges faster than a binary search (see Details), but each step is computationally more demanding. This Demonstration provides an interactive graphical comparison of the two methods on a set of example functions.


	Contributed by: Filip Piękniewski
	Show Initialization Code

In general the secant method (interpolation search) converges faster than the binary search. However there are exceptions to this rule, as shown in the cubic example; the binary search converges neatly, whereas the multiple root causes a derivative to be zero, sending the interpolation far away. Such conditions can be very unfortunate for the secant method, but they can be avoided: multiple roots can be eliminated using algebraic methods, like dividing the polynomial by its derivative.