Finite Difference Approximations of the First Derivative of a Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
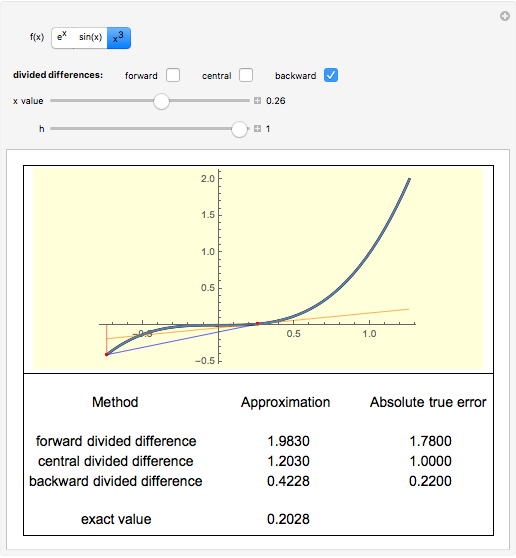
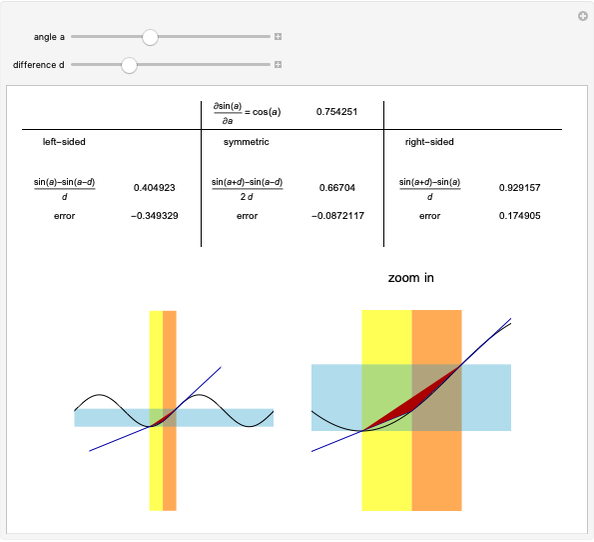
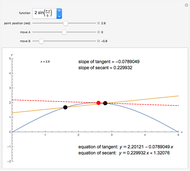
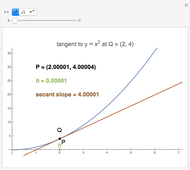
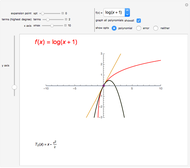
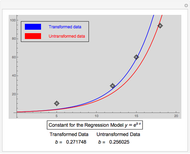
Derivatives of functions can be approximated by finite difference formulas. In this Demonstration, we compare the various difference approximations with the exact value.
Contributed by: Vincent Shatlock and Autar Kaw (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
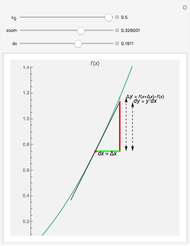
The first derivative of a function 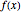 is defined as
is defined as
 .
.
The simplest finite difference formulas for the first derivative of a function are:
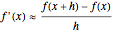 (forward difference)
(forward difference)
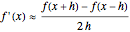 (central difference)
(central difference)
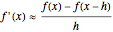 (backward difference)
(backward difference)
Both forward and backward difference formulas have error 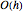 , while the central difference formula has error
, while the central difference formula has error 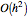 .
.
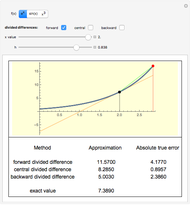
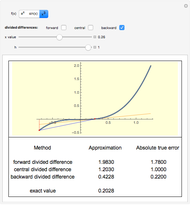
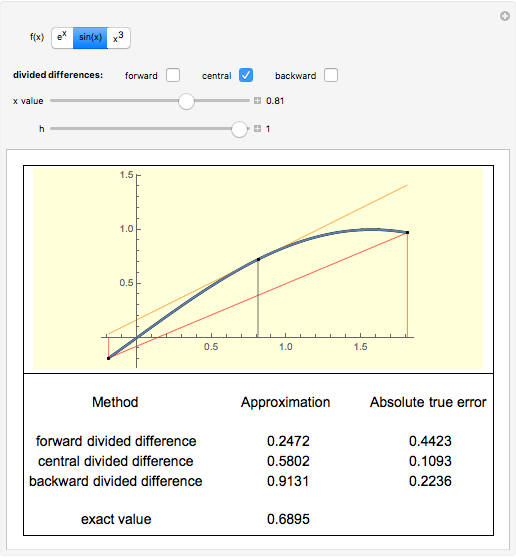
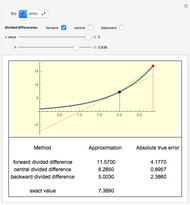
In this Demonstration, we show the difference in values calculated from the three difference formulas and the exact value.
Questions:
1. Does the true error increase proportionally with the step size,  , for the forward and backward difference formulas?
2. Does the true error increase proportionally with the square of the step size,
, for the forward and backward difference formulas?
2. Does the true error increase proportionally with the square of the step size,  , for the central difference formula?
, for the central difference formula?
Reference
[1] A. A. Kaw, D. Nguyen, and E. E. Kalu, Numerical Methods with Applications. http://numericalmethods.eng.usf.edu/publications_book.html.
Permanent Citation