7899
TOPICS
LATEST
ABOUT
AUTHORING AREA
PARTICIPATE
Your browser does not support JavaScript or it may be disabled!
Floating Ball
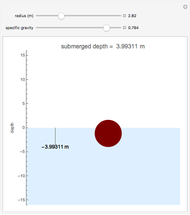
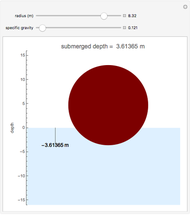
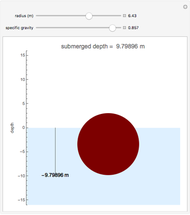
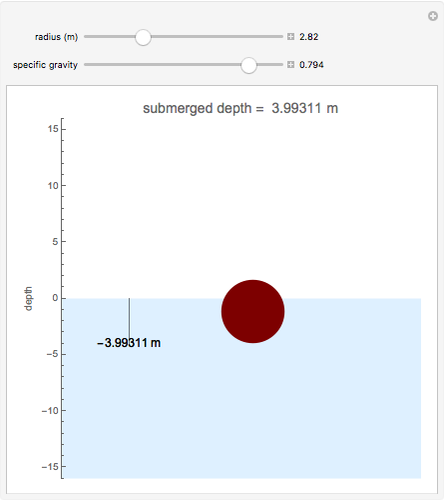
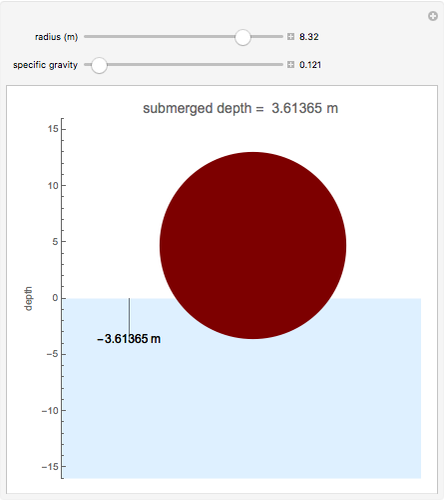
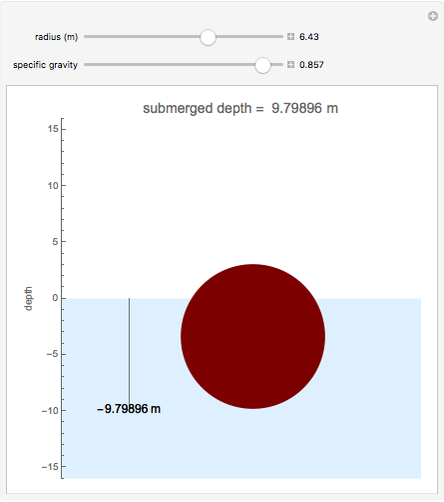
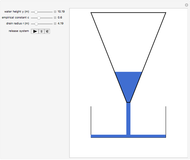
This Demonstration shows how far a floating spherical ball sinks into water by applying Archimedes's principle, calculus, and the solution of nonlinear equations.
Contributed by:
Vincent Shatlock
and
Autar Kaw
THINGS TO TRY
Slider Zoom
Gamepad Controls
Automatic Animation
SNAPSHOTS
DETAILS
The solution runs as follows. Let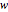
be the weight of the ball and
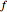be the buoyancy force. Then
.
Let the volume of the ball be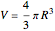
(where
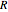is the radius),
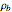be its density
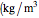), and
be the acceleration due to gravity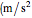
).
The weight of the ball is given by the product of the volume, density, and
:
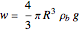
The buoyancy force is given by the weight of water displaced, which is the product of the volume under water and the density of water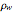
:
,
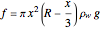where
is the depth to which ball is submerged.
Therefore, with the specific gravity of the ball
, we have
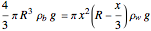, or
.
RELATED LINKS
Equilibrium of a Floating Vessel
(
Wolfram Demonstrations Project
)
Learning Newton’s Method
(
Wolfram Demonstrations Project
)
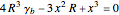PERMANENT CITATION
"
Floating Ball
" from
the Wolfram Demonstrations Project
http://demonstrations.wolfram.com/FloatingBall/
Contributed by:
Vincent Shatlock
and
Autar Kaw
Share:
Embed Interactive Demonstration
New!
Download Demonstration as CDF »
Download Source Code »
(preview »)
Files require
Wolfram
CDF Player
or
Mathematica
.
Related Demonstrations
More by Author
The Principle of Archimedes
Enrique Zeleny
Pascal's Syringe
Enrique Zeleny
Action of a Siphon
Enrique Zeleny
Green's Functions for Diffusion
Brian Vick
Torricelli's Law for Tank Draining
Stephen Wilkerson and Mark Evans (Towson University)
Pitot Tube
Sara McCaslin and Fredericka Brown
Equation of Continuity
Enrique Zeleny
Natatory Bladder of a Fish
Enrique Zeleny
Pascal's Principle
Enrique Zeleny
The Hydraulic Press
Enrique Zeleny
Related Topics
College Physics
Fluid Mechanics
Physics
High School Advanced Calculus and Linear Algebra
High School Mathematics
Browse all topics
Contribute
Make a new version of this Demonstration
Upload a new Demonstration
Note: To run this Demonstration you need Mathematica 7+ or the free Mathematica Player 7EX
Download or upgrade to
Mathematica Player 7EX
I already have
Mathematica Player
or
Mathematica 7+
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
