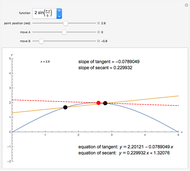
Total Differential of the First Order
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
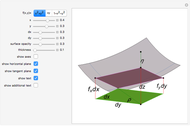
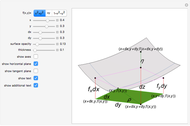
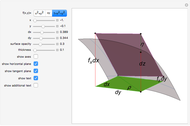
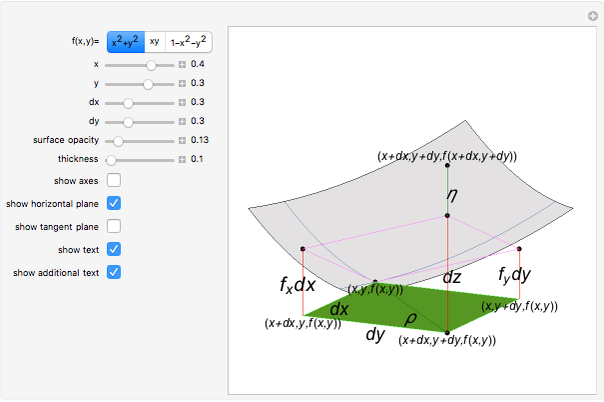
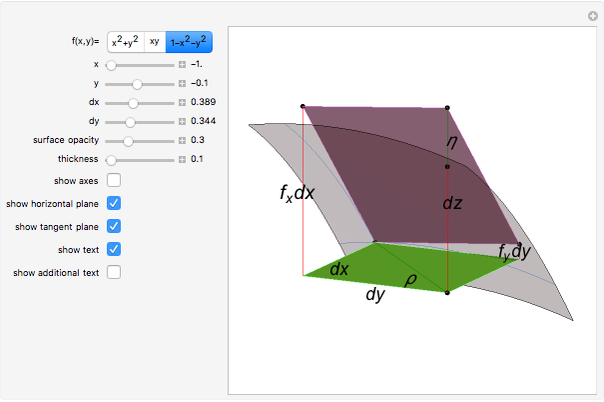
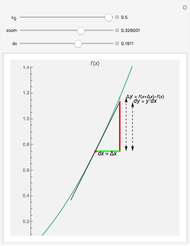
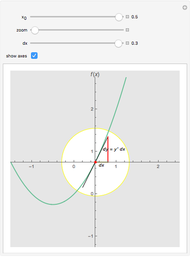
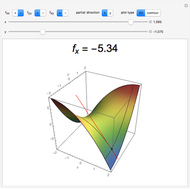
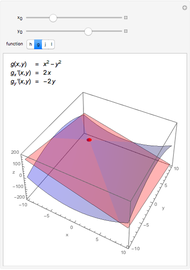
The total differential of a function of two variables is given by definition:  . Then its total increment is given by
. Then its total increment is given by 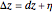 , where
, where  and
and 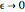 as
as  . The differential
. The differential  is the principal part of
is the principal part of 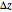 , which means that
, which means that 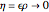 more rapidly than
more rapidly than 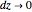 as
as 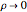 .
.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
 as
as 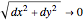 .
.
Permanent Citation