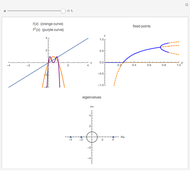
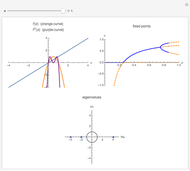
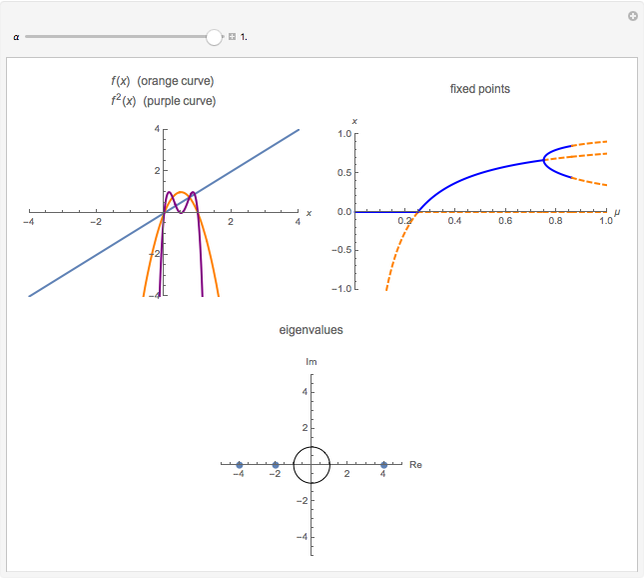
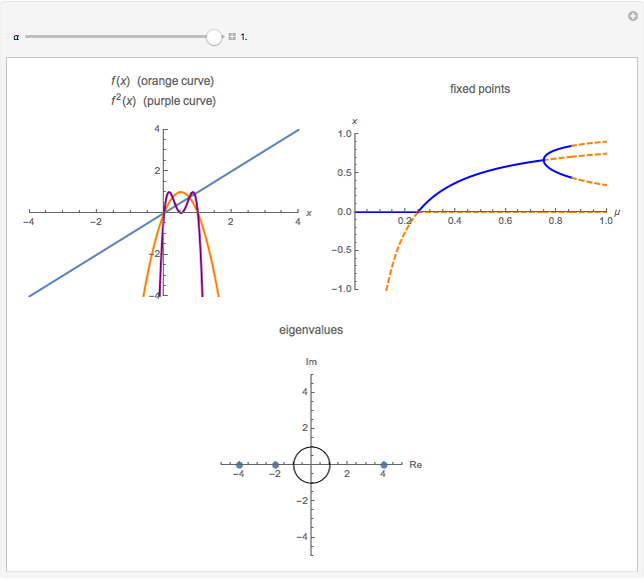
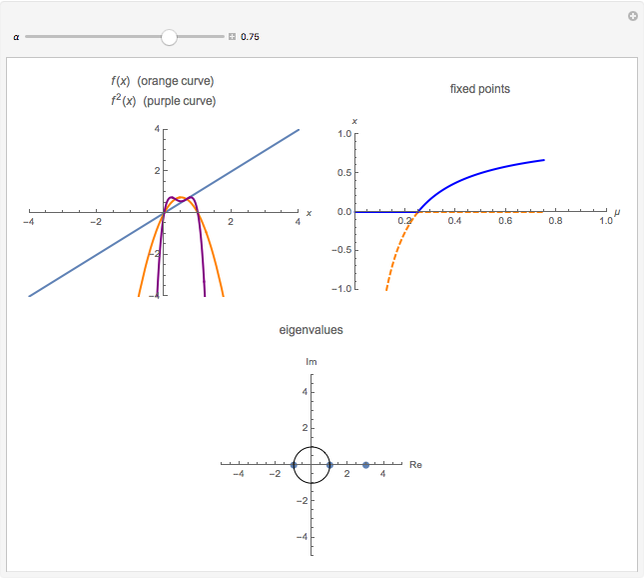
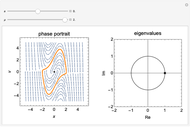
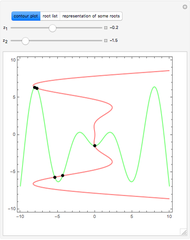
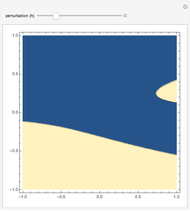
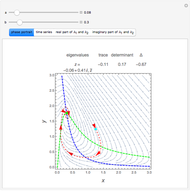
A flip bifurcation occurs when increasing the parameter causes the graph of the function 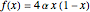or to intersect the line . See Example 2.32 of [1]. In a flip bifurcation, an eigenvalue leaves the unit circle through the point 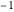. When this happens, the period two points become stable; thus, this is also known as a period-doubling bifurcation. Varying , the zero solution becomes unstable for ; the period one blue branch becomes unstable for 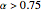; the period-doubling bifurcation occurs at 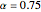. At the period-doubling bifurcation, the fixed points of become stable.