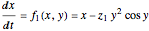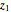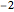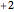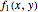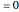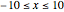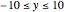Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Steady States for a Dynamical System in 2D

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

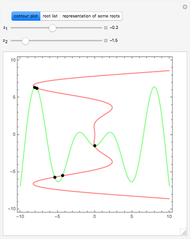
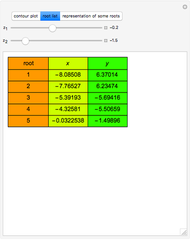
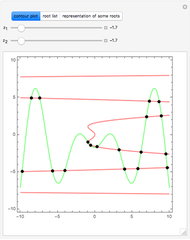
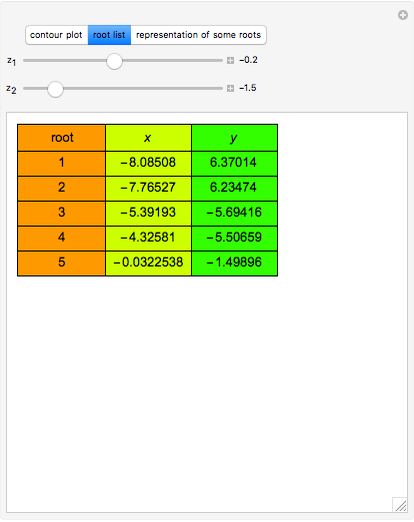
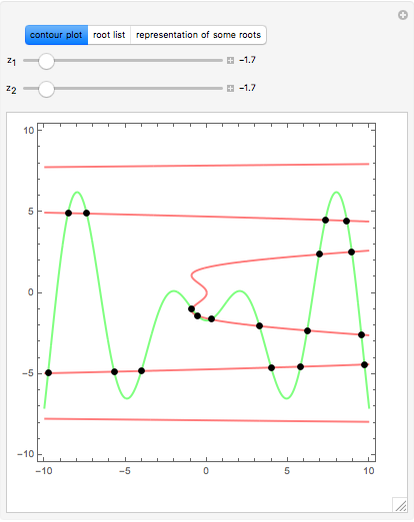
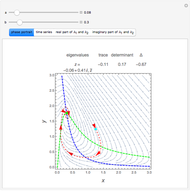
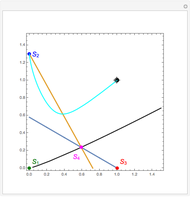
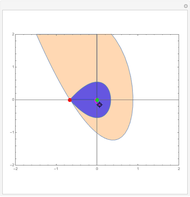
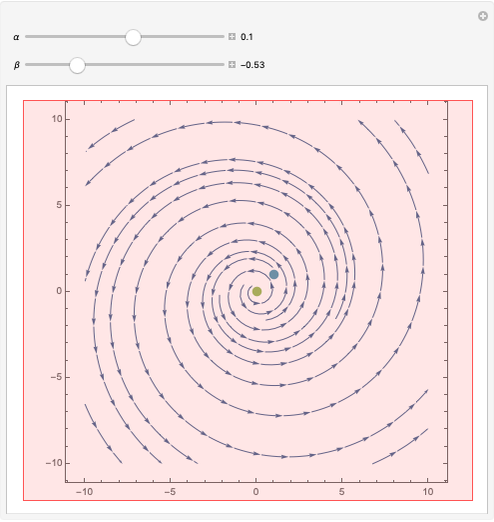
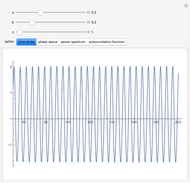
Consider a hypothetical dynamical system governed by the following equations:

[more]

,

,

where and are bifurcation parameters that vary between and and with values set by the user.

The steady states of this system are solutions of the following system of equations:

,

.

The above system of two nonlinear equations exhibits multiple solutions that can all be determined using the built-in Mathematica function ContourPlot [1]. In addition to giving a graphical representation of the contours and and the intersection points (shown in black), this Demonstration provides the numerical values of all roots for and .

[less]

Contributed by: Brian G. Higgins and Housam Binous (June 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] S. Wagon, Mathematica in Action: Problem Solving through Visualization and Computation, 3rd ed., Berlin: Springer–Verlag, 2010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send