Green's Functions for Diffusion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
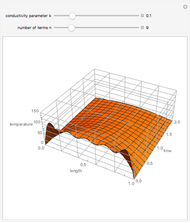
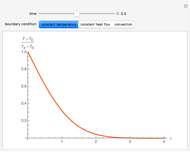
The Green's function is the response to a delta function source with homogeneous boundary conditions. The delta function models a source that is instantaneously pulsed in time and infinitely concentrated in space. The differential equation governing the one-dimensional diffusion Green's function is
[more]
Contributed by: Brian Vick (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
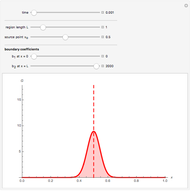
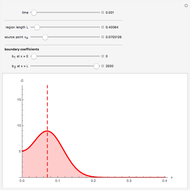
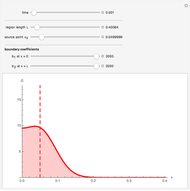
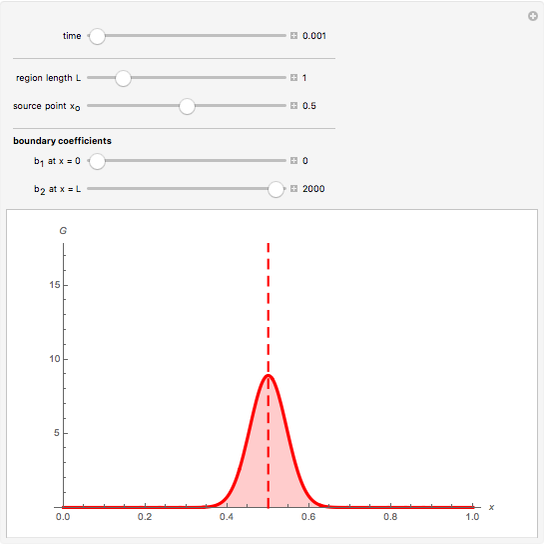
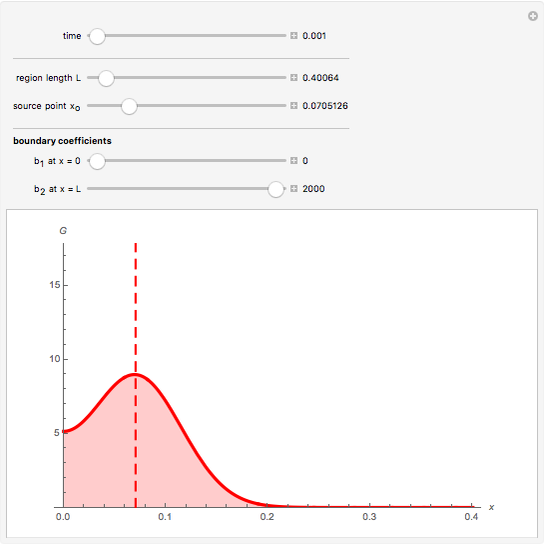
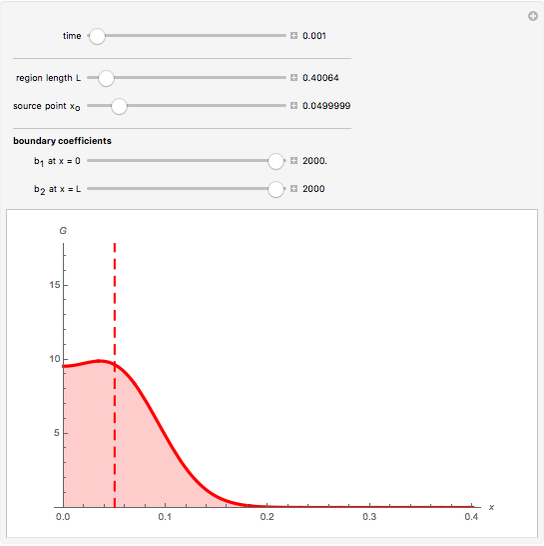
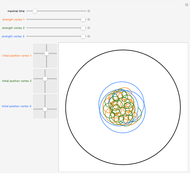
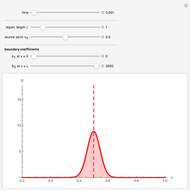
The solution for the Green's function on a finite domain with general boundary conditions is constructed from solutions for an infinite domain using the method of images. In order to see the influence of boundary conditions, place the source point  near a boundary and adjust the boundary parameter,
near a boundary and adjust the boundary parameter,  .
.
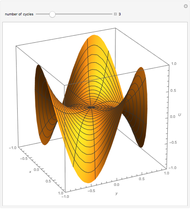
Snapshot 1: the source point is inside the region, far away from boundaries
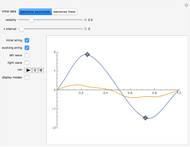
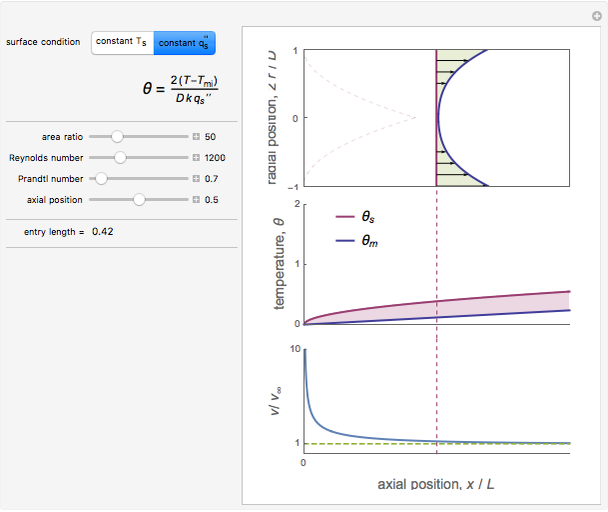
Snapshot 2: the source point is near an insulated boundary ( )
)
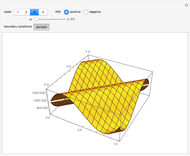
Snapshot 3: the source point is near a zero potential boundary ( large)
large)
Nomenclature:
 = Green's function (1/
= Green's function (1/ )
)
 = position (m)
= position (m)
 = time (s)
= time (s)
 = source location (m)
= source location (m)
 = source time (s)
= source time (s)
 = diffusivity (
= diffusivity ( /s)
/s)
 ,
,  = boundary coefficients (1/m)
= boundary coefficients (1/m)
Permanent Citation