From Vector to Plane

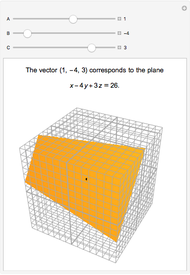
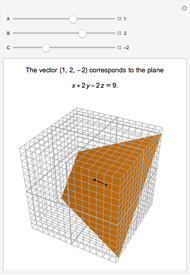
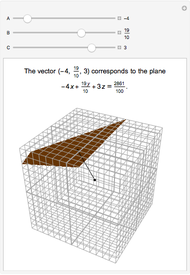
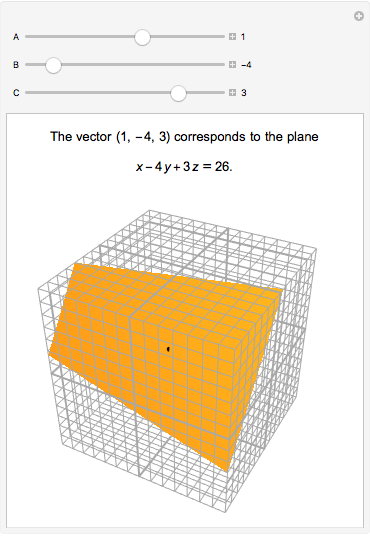
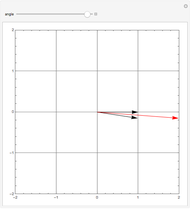
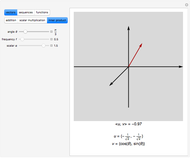
Any nonzero vector defines a unique plane in 3D. Except for planes through the origin, every plane is defined by a unique vector. This vector is normal (perpendicular) to the plane. In the equation of the plane , with as the defining vector, , which is the square of the norm (length) of the vector.

A vector norm is a length. A normal vector is perpendicular to a plane or line.