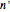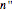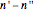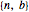Generalized Kaprekar Routine

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
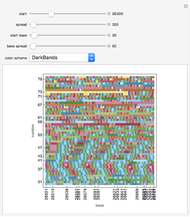
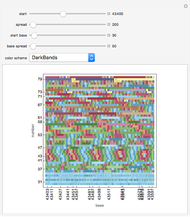
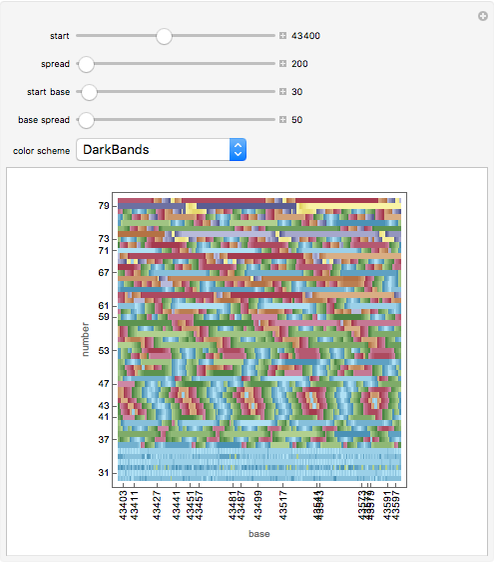
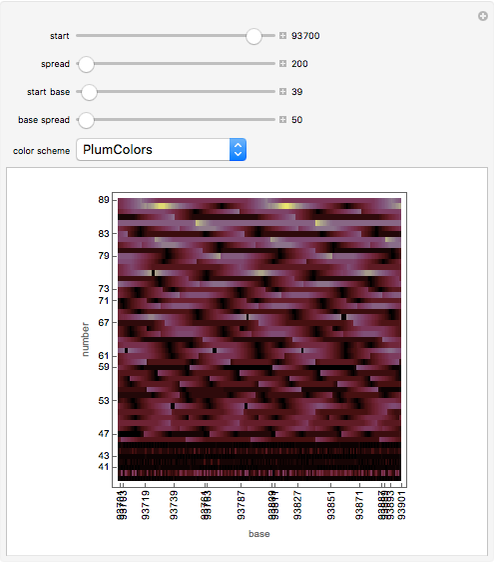
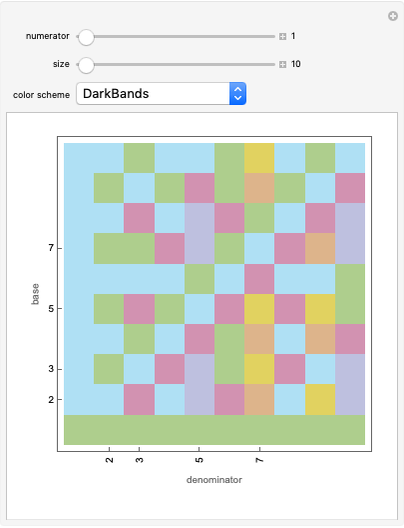
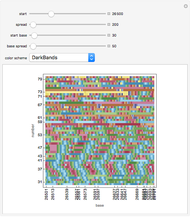
This Demonstration shows fractal patterns in the number of steps required to reach a fixed point or cyclic behavior in an application of Kaprekar's routine applied to the natural numbers for different bases.
[more]
Contributed by: Noel Patson (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Generalized Kaprekar Routine"
http://demonstrations.wolfram.com/GeneralizedKaprekarRoutine/
Wolfram Demonstrations Project
Published: March 7 2011