Equal Incircles along a Line

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
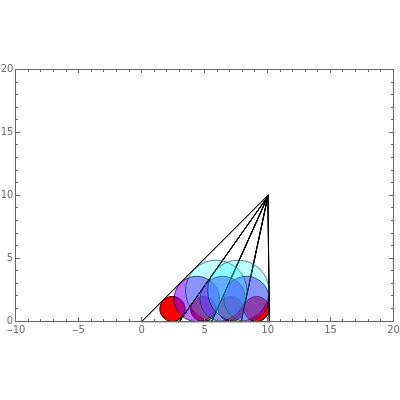
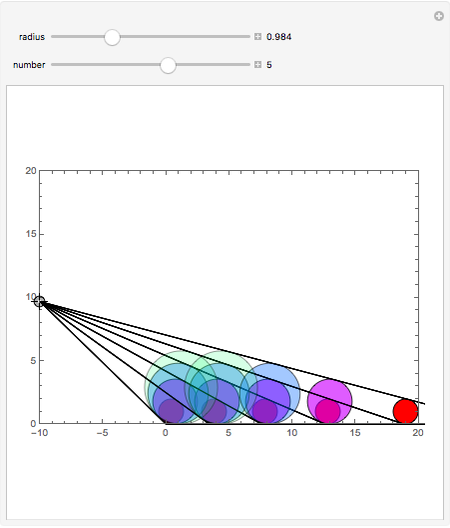
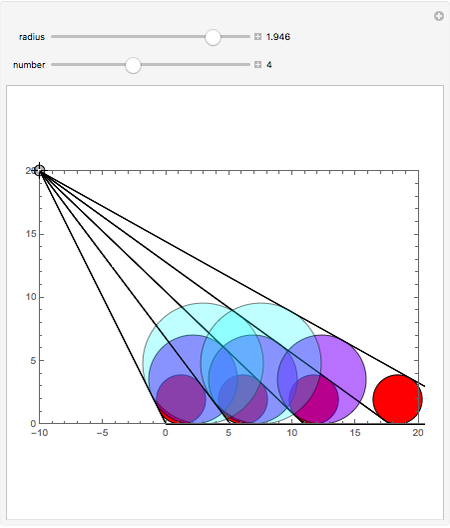
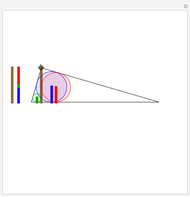
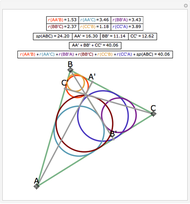
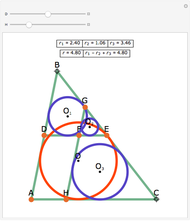
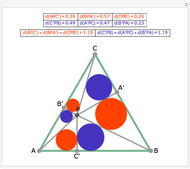
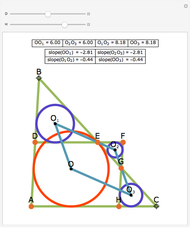
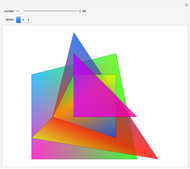
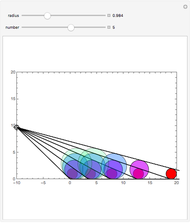
Japanese Sangaku mathematics has a rich history of geometric theorems and problems. The equal incircles theorem is an illustrative example. Consider the incircle 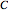 of radius
of radius  of any triangle (each side of the triangle is tangent to the circle) and the extended line
of any triangle (each side of the triangle is tangent to the circle) and the extended line  along one side of the triangle. Construct a triangle with base common to
along one side of the triangle. Construct a triangle with base common to 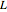 and an incircle of radius
and an incircle of radius  on either side of the triangle. Continue this process on either side of the group of triangles until
on either side of the triangle. Continue this process on either side of the group of triangles until  triangles are constructed,
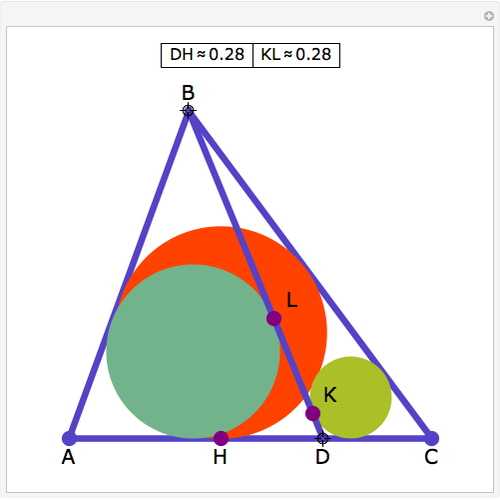
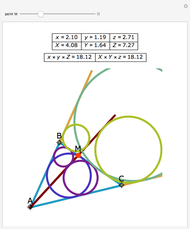
triangles are constructed, 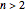 . The incircle of the triangle formed by the combination of any
. The incircle of the triangle formed by the combination of any  ,
,  , adjacent triangles taken from the group of
, adjacent triangles taken from the group of  individual triangles has the same radius as the incircle of the triangle formed by any other
individual triangles has the same radius as the incircle of the triangle formed by any other  adjacent triangles.
adjacent triangles.
Contributed by: Noel Patson (March 2011)
Open content licensed under CC BY-NC-SA
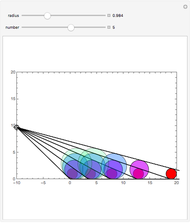
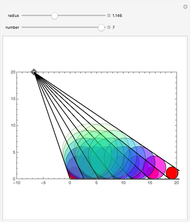
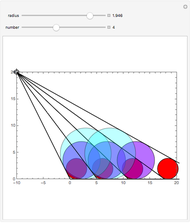
Snapshots
Details
Inspired by Equal incircles theorem.
Permanent Citation
"Equal Incircles along a Line"
http://demonstrations.wolfram.com/EqualIncirclesAlongALine/
Wolfram Demonstrations Project
Published: March 7 2011