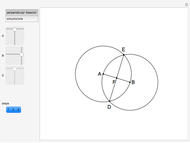
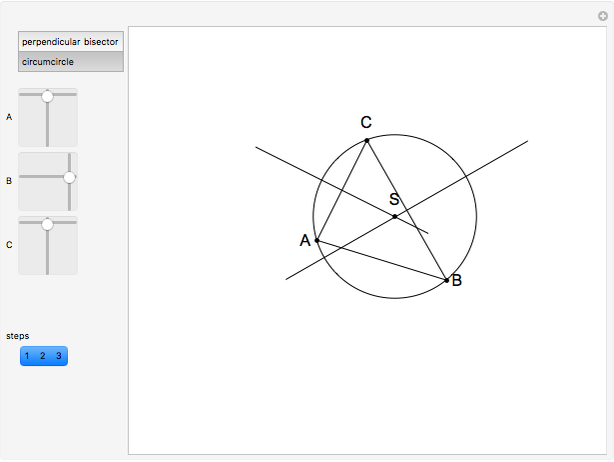
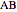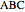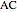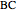Given a Segment, Construct Its Perpendicular Bisector; Given a Triangle, Construct Its Circumcircle
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
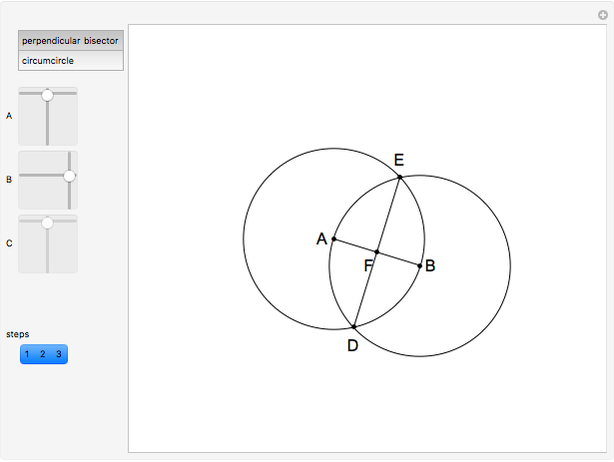
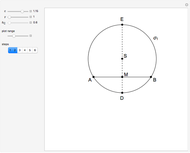
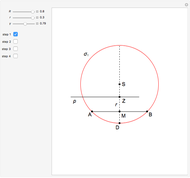
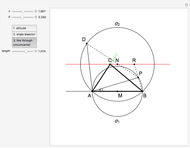
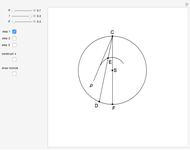
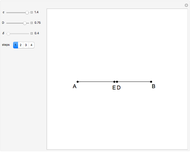
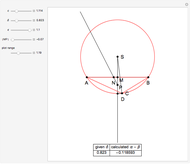
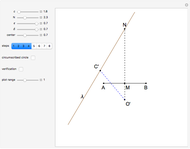
This Demonstration shows two constructions:
[more]
Contributed by: Izidor Hafner (October 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Euclid I. 10. Construct the midpoint of a given segment.
Euclid IV. 5. About a given triangle, circumscribe a circle.
Reference
[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998, pp. 4–5.
Permanent Citation