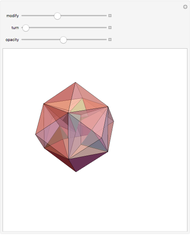
Graph of a Six-Cube and Skeleton of a Rhombic Triacontahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
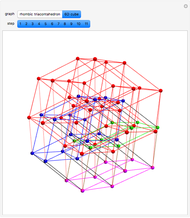
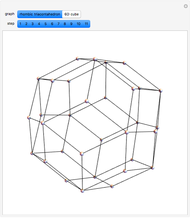
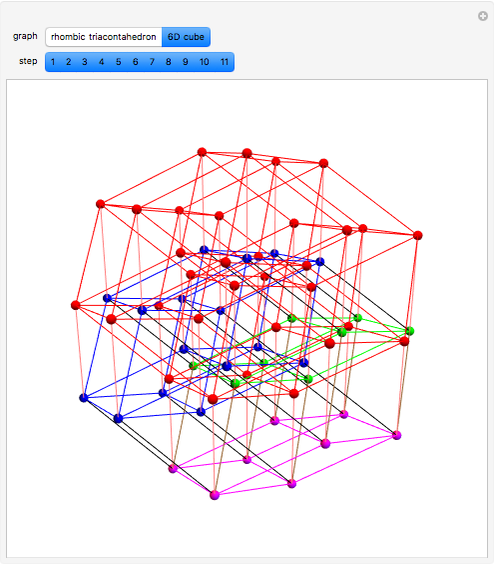
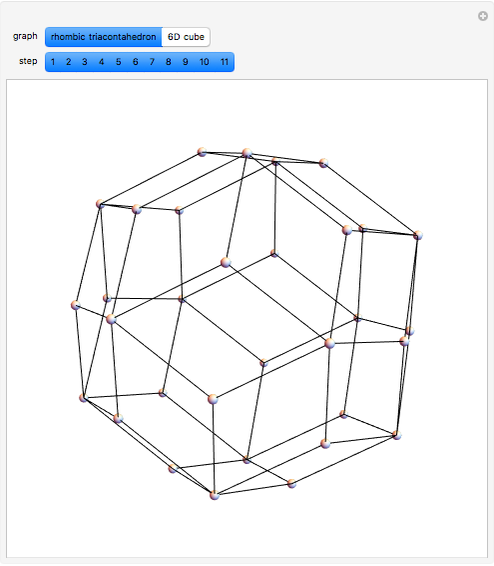
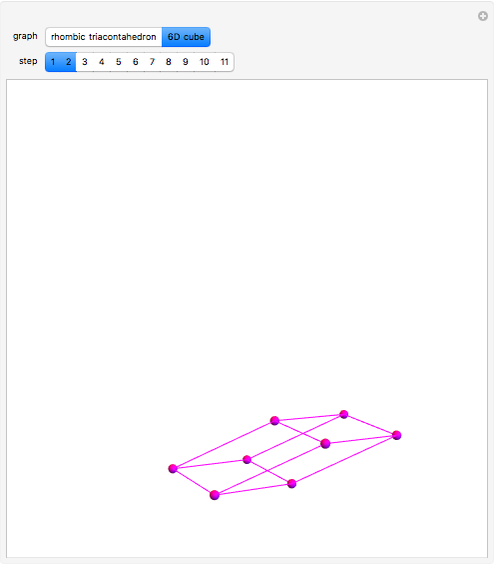
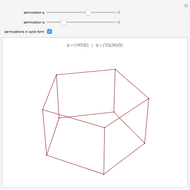
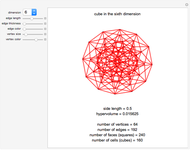
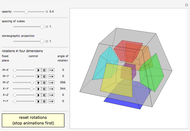
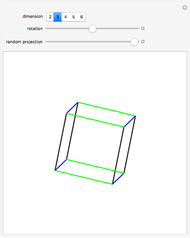
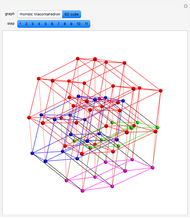
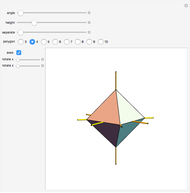
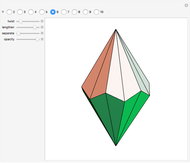
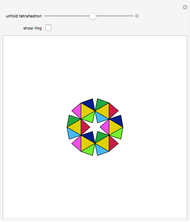
This Demonstration shows the constructions of a graph of a six-cube and the skeleton of a rhombic triacontahedron.
Contributed by: Gábor Gévay, Izidor Hafner and Tomazv Pisanski (September 2019)
Open content licensed under CC BY-NC-SA
Details
The skeleton of the rhombic triacontahedron can be considered as a subgraph of the graph of the six-dimensional cube.
We demonstrate this relationship by showing a representation of the six-cube graph in three-dimensional space with the following properties: 32 of the 64 vertices, 60 of the 192 edges and 30 of the 240 faces of the six-cube are drawn as the vertices, edges and faces, respectively, of the rhombic triacontahedron.
The remaining vertices, edges and faces of the six-cube fall into the interior of the triacontahedron.
This representation can be realized at the cost of some distortions: the square faces of the six-cube are distorted to parallelograms (in particular, those appearing as faces of the triacontahedron will be rhombuses).
References
[1] H. S. M. Coxeter, Regular Polytopes, London: Methuen, 1948.
[2] P. R. Cromwell, Polyhedra, Cambridge, UK: Cambridge University Press, 1997.
[3] G. Gévay, "Icosahedral Morphology," Fivefold Symmetry (I. Hargittai, ed.), Singapore: World Scientific, 1992, pp. 177–203. doi:10.1142/9789814439497_0012.
Snapshots
Permanent Citation