Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Loxodrome

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

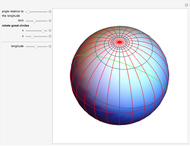
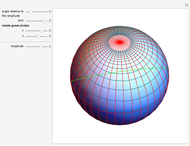
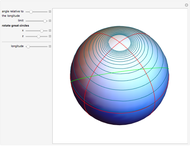
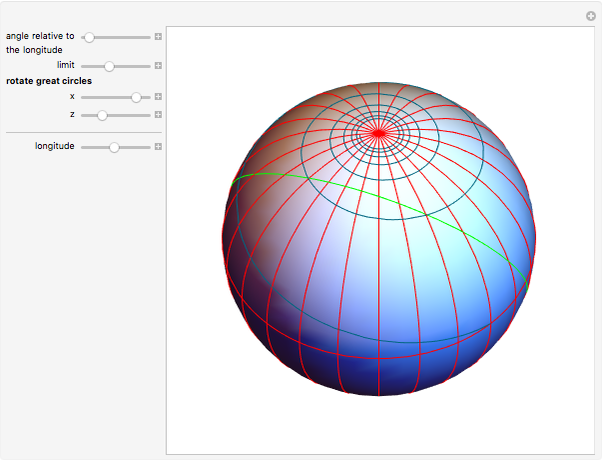
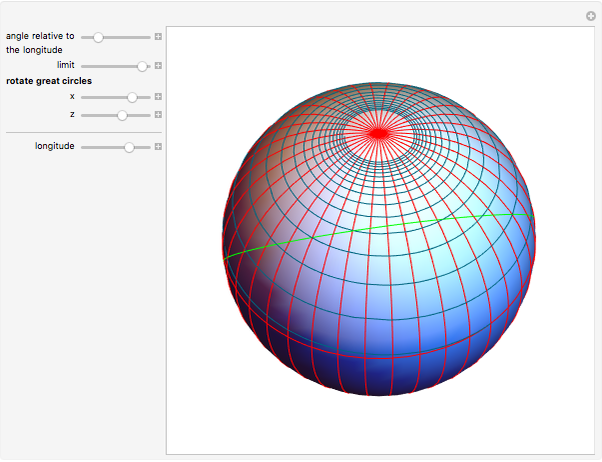
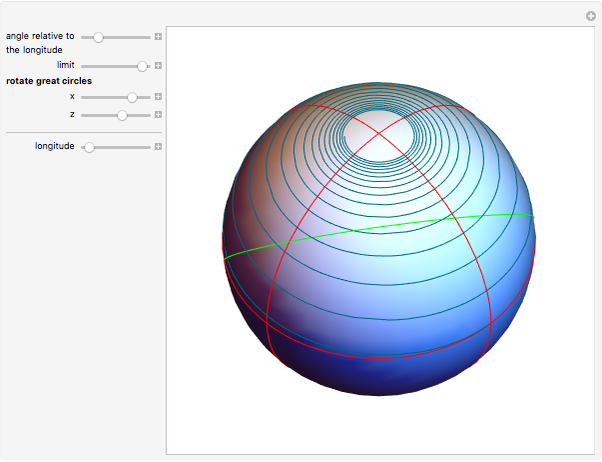
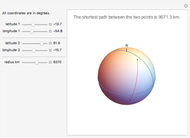
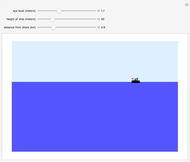
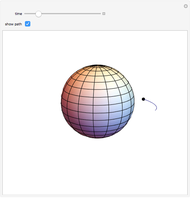
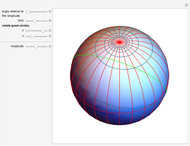
If a point moves on the surface of a sphere so that it maintains a constant angle to a pole, then its path follows a spherical spiral (or a rhumb line). On a general surface of revolution, a point making a constant angle with the the meridians (the intersections of the surface and the planes through the axis) follows a curve called a loxodrome.

Contributed by: Sándor Kabai and Gábor Gévay (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

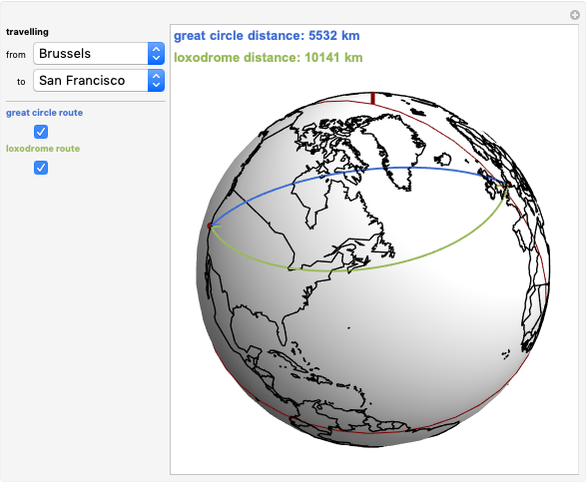
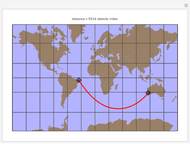
The travel direction is a tangent to the curve, and the direction of the pole is represented by great circles running through the pole (longitudes). A ship or an airplane follows such a curve when the compass bearing is kept constant. As a result, navigation along a loxodrome is easy, but it is not the shortest path. The shortest distance between two points is represented by a great circle running through the two points. A loxodrome is a straight line on a Mercator projection map and a logarithmic spiral on a stereographic projection map.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send