Hydrogen and Lithium Orbitals Using a Hartree Eigenvalue Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
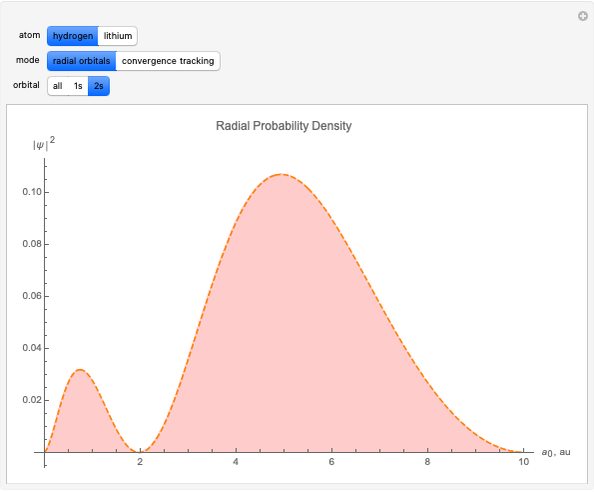
This Demonstration shows how to numerically calculate radial 1s and 2s orbitals of hydrogen and lithium. A Hartree eigenvalue method is applied to a 300×300 square matrix with a step size of  au. The method uses the fact that the interaction potential between electrons can be simplified significantly for simple atoms. Numerically solving for eigenvalues and eigenfunctions of the Schrödinger equation with such a potential is carried out using an iterative process.
au. The method uses the fact that the interaction potential between electrons can be simplified significantly for simple atoms. Numerically solving for eigenvalues and eigenfunctions of the Schrödinger equation with such a potential is carried out using an iterative process.
Contributed by: Nikita M. Kostylev (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To find the solution of a simplified Schrödinger equation for  (
( ), we can simply determine numerical eigenvalue solutions to
), we can simply determine numerical eigenvalue solutions to
 .
.
 is defined as:
is defined as:
 ,
where the potential
,
where the potential  is the interaction potential. It can be approximated [1] by
is the interaction potential. It can be approximated [1] by
 ,
,
where  is the charge, spherically symmetrical and assuming it acts as a Gaussian surface:
is the charge, spherically symmetrical and assuming it acts as a Gaussian surface:
 .
.
Establishing a transformation matrix that would represent the Hamiltonian, using three-point first- and second-order numerical derivatives for the Laplacian and solving iteratively for eigenvalues and eigenvectors generates the approximate solutions for radial density functions.
With "radial orbitals" selected, you can choose to view the calculated normalized radial orbital probability distribution functions for hydrogen or lithium atoms.
With orbital "1s" or "2s" selected, you can also view the calculated numerical value for the associated energies by mousing over the curve.
Reference
[1] C. J. Foot, Atomic Physics, New York: Oxford University Press, 2005.
Permanent Citation