Exact and Approximate Relativistic Corrections to the Orbital Precession of Mercury

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Accounting for the anomaly in the perihelion precession of Mercury provided early support for Einstein's General Theory of Relativity [1]. Very conveniently, accurate astronomical data was already available. Schwarzschild's solution to Einstein's gravitational field equations can be approximated by Newtonian gravity perturbed by a short-range term of magnitude proportional to the Schwarzschild radius  , where
, where 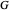 is the universal gravitational constant,
is the universal gravitational constant,  is the attracting mass (the Sun) and
is the attracting mass (the Sun) and  is the speed of light [2, 3].
is the speed of light [2, 3].
Contributed by: Brad Klee. (September 2016)
Open content licensed under CC BY-NC-SA
Details
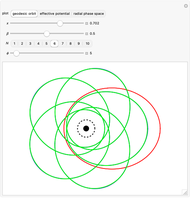
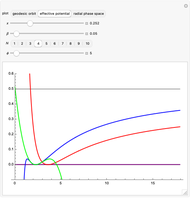
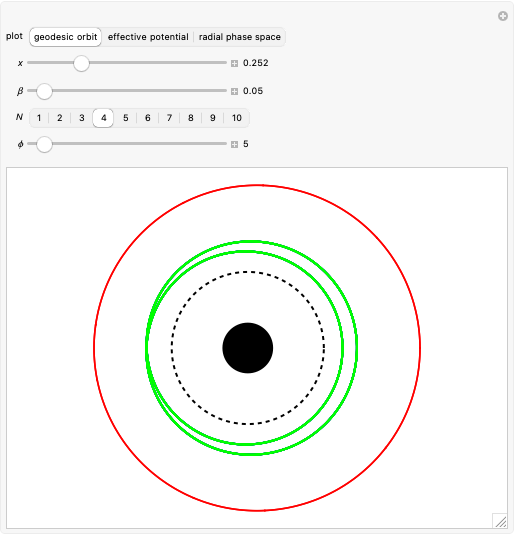
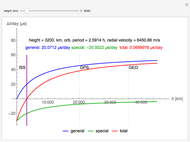
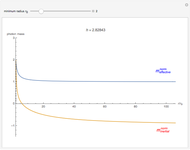
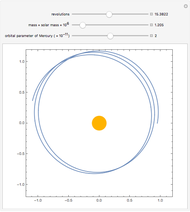
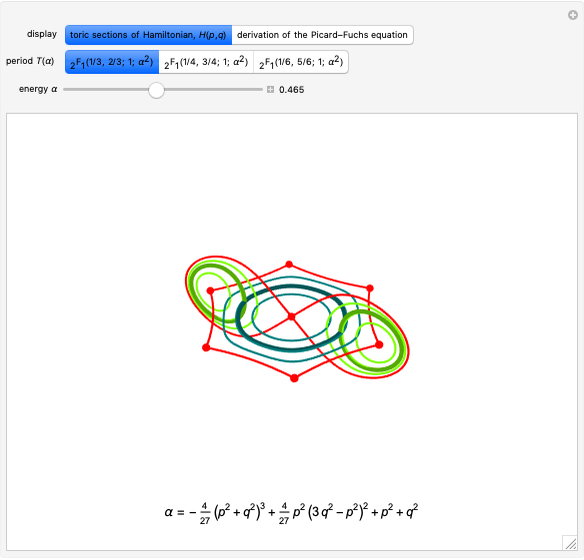
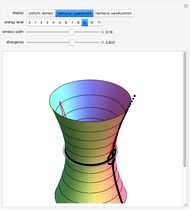
In all plots, blue shows the exact solution, green shows the arbitrary-precision approximation and red shows the classical Kepler/Newton approximation.
In this computation, we set  and
and  . Then the effective radial potential is:
. Then the effective radial potential is:

with minimum at
 ,
,
where we introduce the normalized parameter

restricted to the range 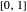 . Expanding the potential around the minimum gives
. Expanding the potential around the minimum gives
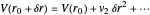
with
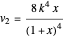 .
.
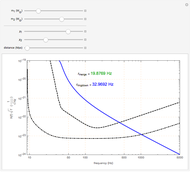
The frequency 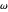 of small oscillations is then given by
of small oscillations is then given by
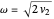 .
.
Taking the first-order term from the Big Precession Equation (see Estimating Planetary Perihelion Precession) and substituting in values for  , we obtain [8]:
, we obtain [8]:
 .
.
This is the simplest exact form for zero-order precession. As 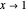 and
and 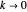 , then
, then  and there is no precession. As
and there is no precession. As 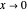 and
and  , then
, then  . In terms of the effective potential, the divergence occurs as the local minimum nears the local maximum and the curve flattens out. The local max and min coincide when
. In terms of the effective potential, the divergence occurs as the local minimum nears the local maximum and the curve flattens out. The local max and min coincide when 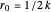 . The Schwarzschild radius is at
. The Schwarzschild radius is at 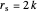 . At the critical point,
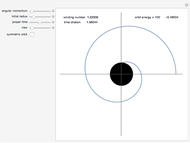
. At the critical point, 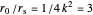 gives the relative radius of the innermost stable circular orbit (isco), depicted as a dashed black line around the black hole in the orbit graphs. The prediction that
gives the relative radius of the innermost stable circular orbit (isco), depicted as a dashed black line around the black hole in the orbit graphs. The prediction that  provides a test for all solutions: as
provides a test for all solutions: as 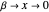 , the orbit should approach no closer to
, the orbit should approach no closer to  than
than 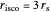 .
.
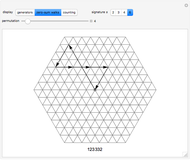
Other authors [9-11] discuss aesthetically pleasing solutions that arise from a conspiracy of parameters, as occurs with 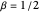 ,
, 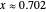 . It is possible to write an algorithm that operates on the approximate solution, a particular value for
. It is possible to write an algorithm that operates on the approximate solution, a particular value for  and a rational number
and a rational number 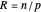 ,
,  , that returns an approximate solution for the
, that returns an approximate solution for the  value, ultimately by finding the root of a polynomial equation. Acceptable values close to
value, ultimately by finding the root of a polynomial equation. Acceptable values close to 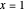 can be found quickly using a linear procedure because
can be found quickly using a linear procedure because
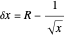
is a small number. For example for 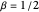 and
and  ,
, 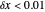 . Doing a quick search, we obtain the following approximate "Magic Numbers":
. Doing a quick search, we obtain the following approximate "Magic Numbers":
$Failed
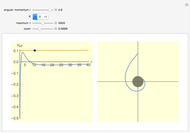
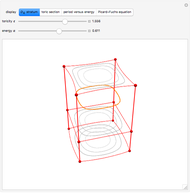
Exploring these sequences shows interesting properties of closed orbits. We see that each figure has  -fold dihedral symmetry with
-fold dihedral symmetry with  crossing points.
crossing points.
From a mathematical perspective, it would be interesting to extend the precision measurement of  values, prove the empirical crossing formula and give a physical characterization of the crossing points using the full equations of motion, but physicists will be more interested in comparing predictions with data. Planetary precession calculations often use only the zero-order precession terms. For example, Mercury has
values, prove the empirical crossing formula and give a physical characterization of the crossing points using the full equations of motion, but physicists will be more interested in comparing predictions with data. Planetary precession calculations often use only the zero-order precession terms. For example, Mercury has
 ,
,
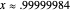 ,
,
which implies
 arcseconds per Julian century.
arcseconds per Julian century.
Substituting  , this Demonstration shows that a Kepler/Newton approximation is almost good enough to describe an isolated Mercury-Sun system on the order of one year. In more extreme gravity, the zero-order approximation fails, and higher-order energy dependence needs to be considered. This is an exciting opportunity, as humankind continues to develop incredible new experiments in black hole astronomy [2, 6].
, this Demonstration shows that a Kepler/Newton approximation is almost good enough to describe an isolated Mercury-Sun system on the order of one year. In more extreme gravity, the zero-order approximation fails, and higher-order energy dependence needs to be considered. This is an exciting opportunity, as humankind continues to develop incredible new experiments in black hole astronomy [2, 6].
References
[1] A. Einstein, "Erklärung der Perihelionbewegung der Merkur aus der allgemeinen Relativitätstheorie." Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 1915 pp. 831–839. (Sep 27, 2016) einsteinpapers.press.princeton.edu/vol6-doc/261. English translation: einsteinpapers.press.princeton.edu/vol6-trans/128?ajax.
[2] J. A. Wheeler, A Journey into Gravity and Spacetime, New York: W. H. Freeman and Co., 1990 pp. 168–183.
[3] R. M. Wald, General Relativity, Chicago: University of Chicago Press, 1984 pp. 139–143.
[4] K. Weierstrass, "Zur Theorie der elliptischen Functionen," Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 1882. (Sep 28, 2016) archive.org/stream/mathematischewer02weieuoft#page/244/mode/2up.
[5] M. Abramowitz and I. A. Stegun (eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, 1965. (Sep 28, 2016) people.math.sfu.ca/~cbm/aands/page_627.htm.
[6] G. Scharf. "Schwarzschild Geodesics in Terms of Elliptic Functions and the Related Red Shift." arxiv.org/abs/1101.1207.
[7] B. Klee. "Plane Pendulum and Beyond by Phase Space Geometry." arxiv.org/abs/1605.09102.
[8] F. Frohlich. "Another Planetary Sequence" (thread). SeqFan. (Sep 11, 2016) list.seqfan.eu/pipermail/seqfan/2016-September/016731.html.
[9] P. Erdös, "Spiraling the Earth with C. G. J. Jacobi," American Journal of Physics, 68(10), 2000 pp. 888–895. doi:10.1119/1.1285882.
[10] W. G. Harter. "Classical Mechanics with a Bang!," Unit 3, p. 46. (Sep 28, 2016) www.uark.edu/ua/modphys/markup/CMwBang_Info_ 2016.html.
[11] S. Wolfram, "Black Hole Tech?," from Stephen Wolfram Blog—A Wolfram Web Resource. (Sep 28, 2016) blog.stephenwolfram.com/2016/02/black-hole-tech.
Snapshots
Permanent Citation