Kenyon Tiling Construction (Substitution)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
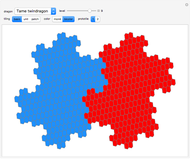
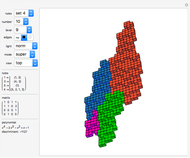
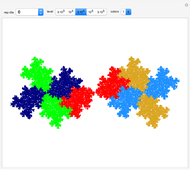
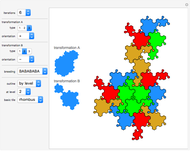
This Demonstration shows how to create approximations to fractals by tile substitutions, using Kenyon's construction with self-similar tilings.
Contributed by: Dieter Steemann (March 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
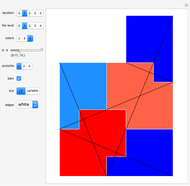
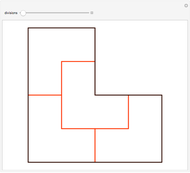
Kenyon [1] gives an explicit construction for self-similar tilings based on complex Perron numbers  that satisfy
that satisfy  where
where  ,
,  and
and  are natural numbers. His method creates a closed polygonal path that can be filled by parallelograms (prototiles) with edges related to the vectors
are natural numbers. His method creates a closed polygonal path that can be filled by parallelograms (prototiles) with edges related to the vectors  . The iteration of this method converges to a fractal boundary.
. The iteration of this method converges to a fractal boundary.
This Demonstration shows the tiling of such boundaries by parallelograms for fixed  and five chosen combinations of
and five chosen combinations of  ,
,  and
and  . The iterated substitution is extended so that prototiles at every iteration level can be merged into super-tiles that also tile the boundary of higher iteration levels.
. The iterated substitution is extended so that prototiles at every iteration level can be merged into super-tiles that also tile the boundary of higher iteration levels.
Controls
 : Use this popup menu to select the set of polynomial coefficients.
: Use this popup menu to select the set of polynomial coefficients.
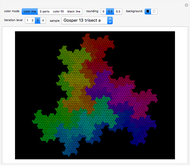
depth: Use this slider to set the iteration. At  only prototiles are shown; higher levels approximate the boundary fractal by substitution of prototiles.
only prototiles are shown; higher levels approximate the boundary fractal by substitution of prototiles.
super: Use this slider to select the iteration level where the prototiles are merged to super-tiles. At  the basic tiling by parallelograms is shown.
the basic tiling by parallelograms is shown.
tile: Use this popup menu to select one of the three tile types; at higher levels, the tiles may become similar.
Approximations of well-known fractals are achieved by setting the parameters to:
 ,
,  → Kenyon 121 fractal [2]; this is the example given in [1].
→ Kenyon 121 fractal [2]; this is the example given in [1].
 ,
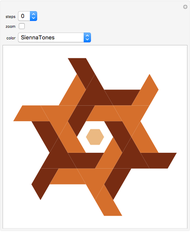
,  → Rauzy fractal.
→ Rauzy fractal.
{ ,
,  → ammonite (curly) fractal.
→ ammonite (curly) fractal.
The corresponding generation of tiling boundaries is part of the Demonstration Kenyon Tiling Construction (Boundary) in the Related Links.
References
[1] R. Kenyon, The Construction of Self-Similar Tilings," Geometric & Functional Analysis, 6(3), 1996 pp. 471–488. doi:10.1007/BF02249260.
[2] Tilings Encyclopedia. "Richard Kenyon: Discovered Tilings." (Feb 28, 2018) tilings.math.uni-bielefeld.de/person/richard-kenyon.
Permanent Citation