Ammann Tiling A4

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
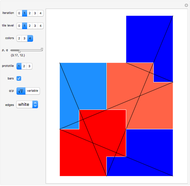
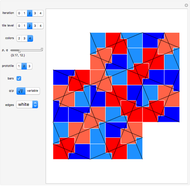
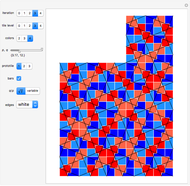
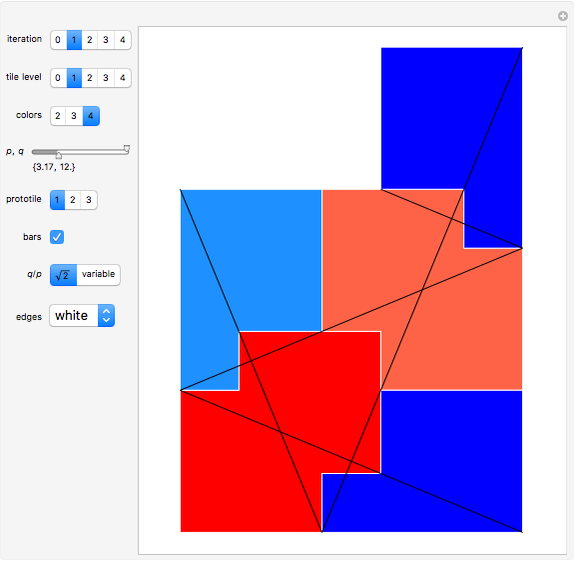
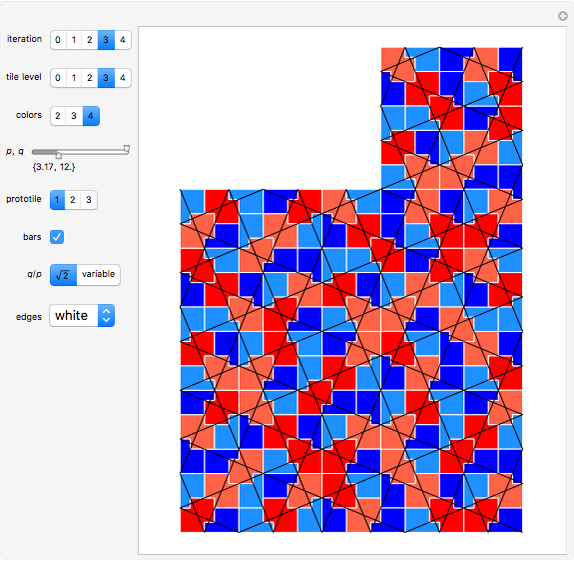
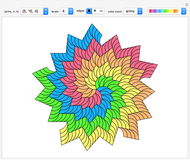
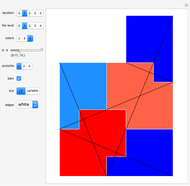
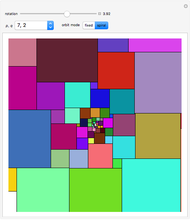
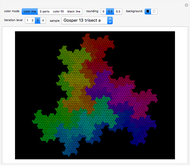
This Demonstration shows a parametrized version of the aperiodic tiling A4 discovered by Robert Ammann in 1977 [1]. The method uses substitution tiling.
Contributed by: Dieter Steemann (July 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In 1977, Robert Ammann [1] discovered a set of aperiodic prototiles later called the set A4 by Grünbaum and Shephard [2]. In order to ensure an aperiodic tiling, the original tiling uses either marked tiles or tiles with indentations that must be filled by keys. This Demonstration does not need keys because the substitution rules force aperiodicity. The parameters 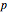 and
and  can have any positive value (limited to the range
can have any positive value (limited to the range 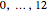 in this Demonstration), but only for
in this Demonstration), but only for  do the Amman bars become straight lines. With increasing iteration levels, the super tiles approach the same shape as obtained directly by setting the parameter ratio to
do the Amman bars become straight lines. With increasing iteration levels, the super tiles approach the same shape as obtained directly by setting the parameter ratio to  , that is, when using this ratio, subsequent super tile shapes are similar.
, that is, when using this ratio, subsequent super tile shapes are similar.
Controls
"iteration" The initial tile (prototile) is shown at iteration level 0; higher levels show iterated super tiles composed of prototiles.
"tile level" Tiles are colored according to the given level as long as it is at most the current iteration level.
"colors" Set the coloring of the involved prototile types.
"prototile" Select one of the three involved prototile types as the initial tile.
"bars"
Use this checkbox to toggle the display of Amman bars; straight lines across the tiling only appear if  .
.
"edges" Use this popup menu to select the color of the prototile edges.
References
[1] Wikipedia. "Robert Ammann." (July 27, 2017) en.wikipedia.org/wiki/Robert_Ammann.
[2] B. Grünbaum and G. C. Shephard, Tilings and Patterns, New York: W. H. Freeman, 1987 pp. 529–530.
Permanent Citation