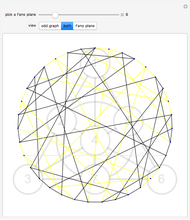
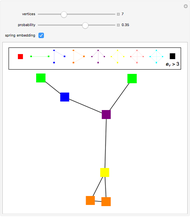
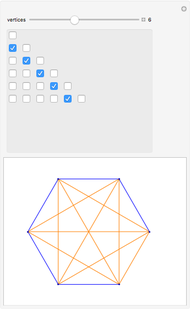
Imagine a set of dominos with strings connecting the dominoes that share a number. Could this mess of strings be laid out nicely? More formally, is there a nice embedding for a graph based on connecting unordered tuples from {1, ..., n}? Graphs of this type are known as Kneser graphs.
Compose the cyclic permutations (12345678) and (13527486) repeatedly: (12345678), (13527486), (15738264), (17856342), (18674523), (16482735), and (14263857). When these are partitioned into unordered tuples, (e.g., (12345678) becomes (12), (34), (56), (78)), each tuple appears exactly once. The permutation (13527486) is thus special. This Demonstration uses preselected permutations to provide nice pictures of these graphs.
Miraculously, these same permutations are used by the Central Council of Church Bell Ringers. For graph order 12 ("Maximus", for a bell ringer) the selected permutations are a partial set.
