Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Koch-Subdivided Polyhedra

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

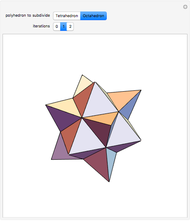
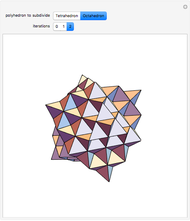
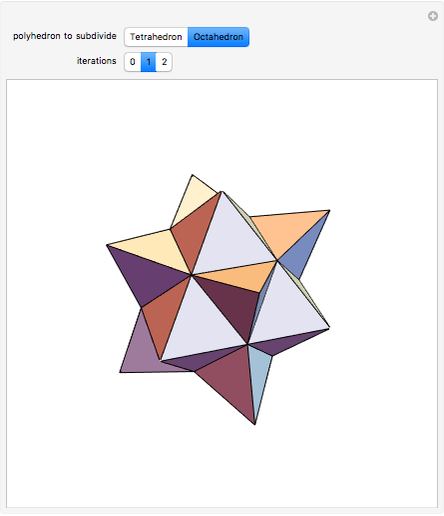
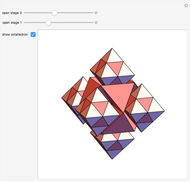
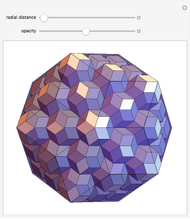
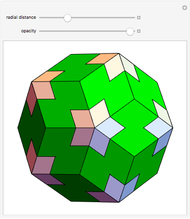
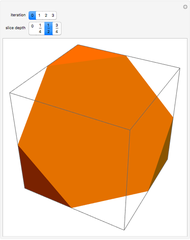
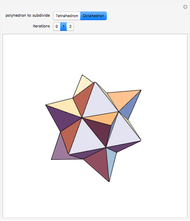
This Demonstration shows a "graftal" technique to subdivide the triangular faces of a polyhedron.

[more]

Many fractal curves can be generated using L-systems or string-rewrite rules, in which successive stages of the curve are generated by replacing each line segment with multiple smaller segments in a particular arrangement.

The same technique can be extended to surfaces, where a stage is constructed by replacing each triangle with multiple smaller triangles. Here we apply this technique to two of the regular polyhedra with triangular faces.

[less]

Contributed by: Stewart Dickson after work by Robert Dickau (September 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Each successive stage is created by dividing each triangle into four smaller triangles, raising the midpoint of the middle triangle, and then closing the surface by building a tetrahedron-shaped shell on the middle triangle. The first iteration on the tetrahedron is Kepler's stella octangula, which is the compound of the tetrahedron and its dual.

Based on the Demonstration Triangular Koch Fractal Surface by Robert Dickau.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send