Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

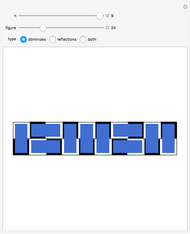
Lattice Path Interpretations

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

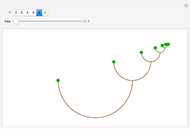
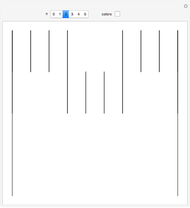
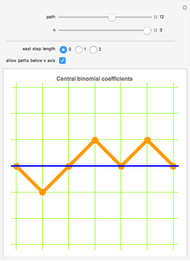
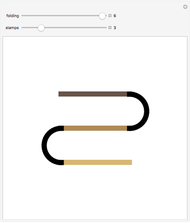
Many famous families of integers can be represented by the number of paths through a lattice given various restrictions. This Demonstration illustrates the various paths from 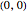to 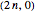using northeast and southeast steps, with the option to permit no eastward steps, single steps east, or double steps east, as well as the option to accept paths dipping below the axis (southeast steps). Counting the paths for the various choices generates six named sequences.

Contributed by: Robert Dickau (March 2008)
Open content licensed under CC BY-NC-SA

Snapshots

Details

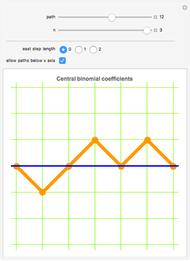
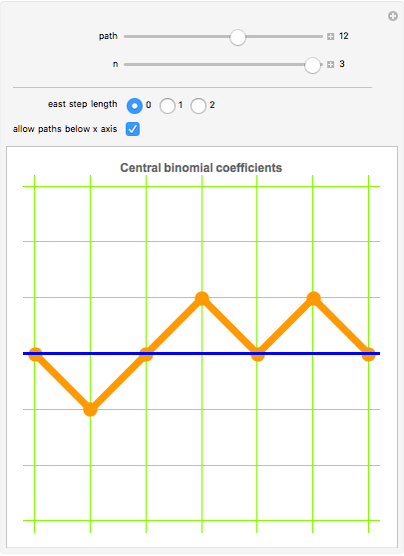
Snapshot 1: paths consisting only of steps northeast and southeast that are allowed to drop below the axis represent the central binomial coefficients—that is, the middle entries in Pascal's triangle

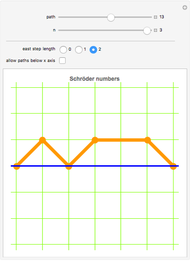
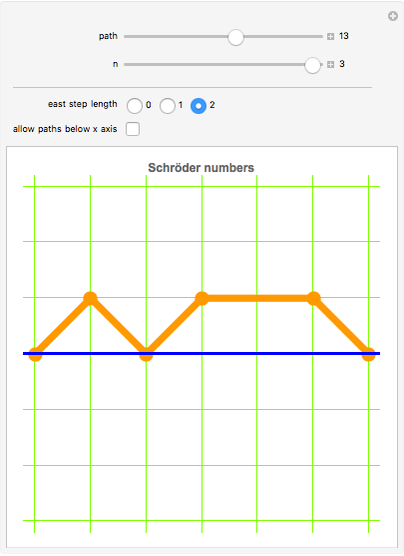
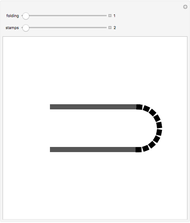
Snapshot 2: paths that do not cross the axis and consist of single steps northeast and southeast and double steps east describe the Schröder numbers

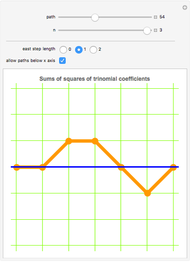
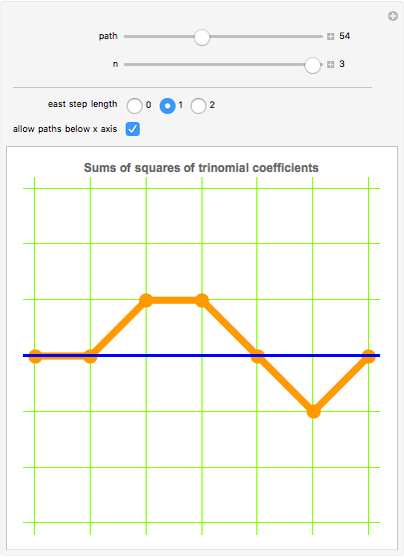
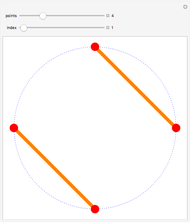
Snapshot 3: paths that can cross the axis and consist only of single steps northeast, southeast, and east are equivalent to the sums of squares of the trinomial coefficients—that is, the coefficients in the expansion of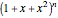

Identification of "sums of squares of trinomial coefficients" (A082758) thanks to the On-Line Encyclopedia of Integer Sequences: oeis.org.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send