Labeled Polygon Triangulations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
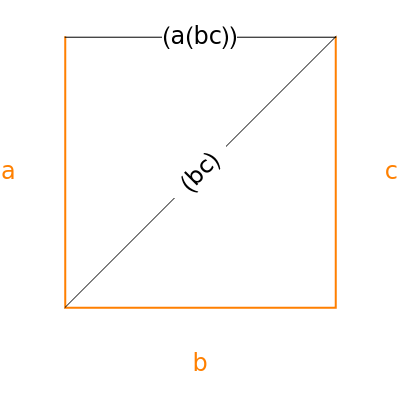
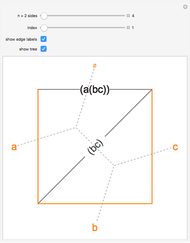
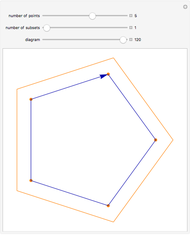
Two interpretations of the Catalan numbers are the number of ways to parenthesize an ordered sequence of numbers to be multiplied, two at a time, and the number of ways a polygon with  sides can be cut into
sides can be cut into  triangles. This Demonstration shows the equivalence of the two interpretations by labeling each polygon triangulation with the corresponding parenthesized expression.
triangles. This Demonstration shows the equivalence of the two interpretations by labeling each polygon triangulation with the corresponding parenthesized expression.
Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
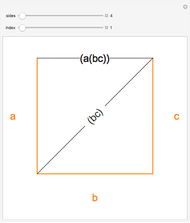
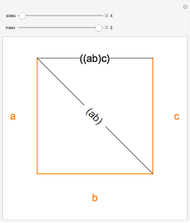
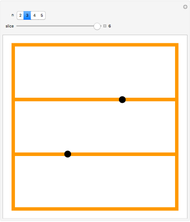
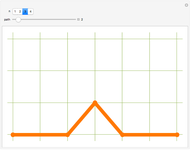
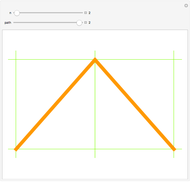
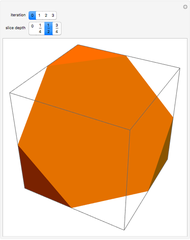
The correspondence is built up by labeling the sides of a polygon. In the parenthesized expression, the innermost pair or pairs of items being multiplied correspond to a new edge drawn from the "beginning" (measuring counterclockwise) of one polygon side to the "end" of the other: edge (bc) in Snapshot 1 and (ab) in Snapshot 2. Another edge is then drawn based on products involving the original pairs: in Snapshot 1, beginning of side a to end of edge (bc), resulting in (a(bc)); in Snapshot 2, beginning of edge (ab) to end of side c, resulting in ((ab)c).
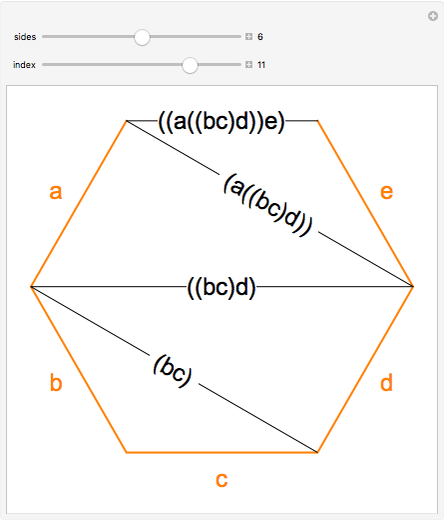
Snapshot 3: the process is repeated until no products remain in the parenthesized expression, at which point the parenthesized expression corresponding to the triangulation appears at the top side of the polygon
M. Gardner, Chapter 20, Time Travel and Other Mathematical Bewilderments, New York: W. H. Freeman, 1988.
Permanent Citation
"Labeled Polygon Triangulations"
http://demonstrations.wolfram.com/LabeledPolygonTriangulations/
Wolfram Demonstrations Project
Published: March 7 2011