Expanded Magnitude Estimation Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
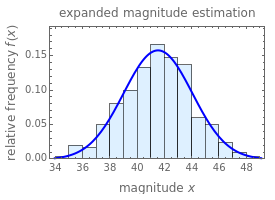
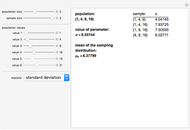
This Demonstration presents an expanded version of the magnitude estimation method used to assess the perceived intensity of physical and chemical stimuli by humans or their preference for a product. It is based on the individual subject or panelist's assessment, not as a single number or equivalent length, but as lower and upper limits of a range. This is followed by Monte Carlo simulations to produce the mean response and its standard deviation. These can also be computed directly from the entered ranges' limits. If the entered minimum equals the entered maximum in all the evaluations, this reduces to the traditional method.
Contributed by: Mark D. Normand and Micha Peleg (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
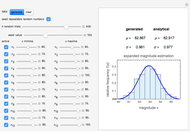
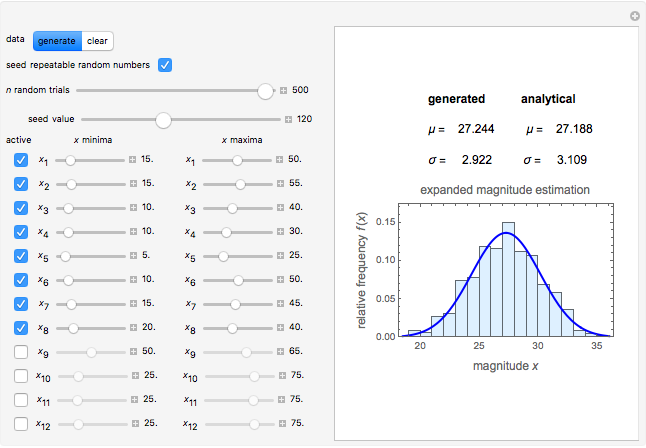
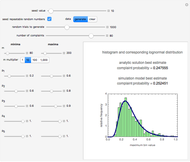
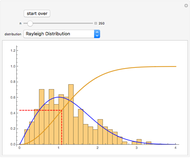
Snapshot 1: twelve relatively high ratings having a relatively small spread
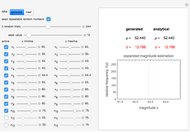
Snapshot 2: eight relatively low ratings having a relatively large spread
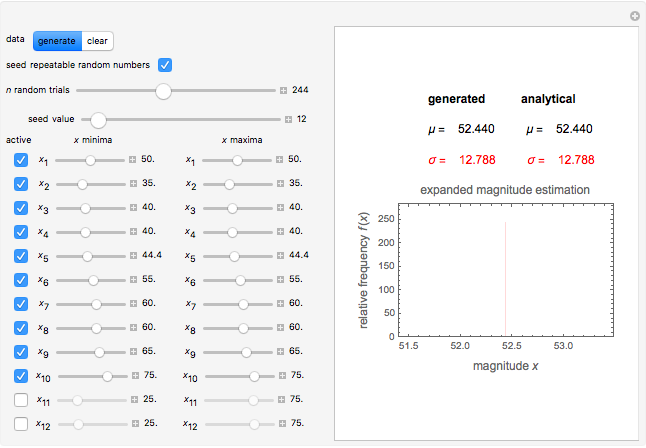
Snapshot 3: ten ratings entered as in the traditional method (all the  minima are equal to their corresponding
minima are equal to their corresponding  maxima)
maxima)
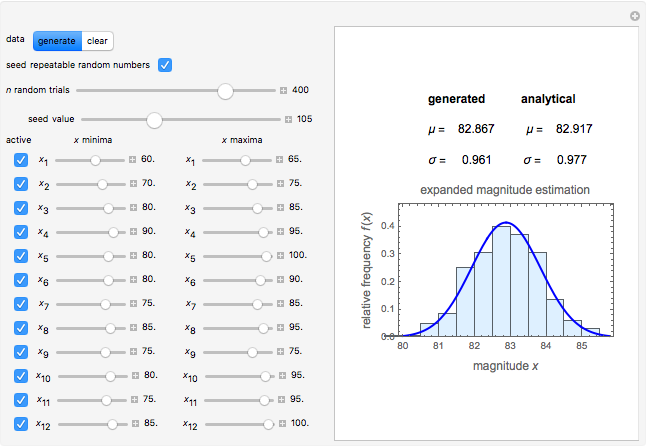
This Demonstration simulates an expanded version of the magnitude estimation method, where the sensory evaluations are entered as lower and upper limits of a range rather than single numbers or equivalent lengths. The calculation of the mean and standard deviation of the entered evaluations is done in two ways for mutual verification:
1. By Monte Carlo simulation, generating and averaging of numerous combinations of values chosen randomly from within the respective intervals. The mean  and standard deviation
and standard deviation  of this generated data are considered as those that correspond to the specified ranges.
of this generated data are considered as those that correspond to the specified ranges.
2. Analytically, using the formulas 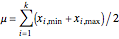 and
and 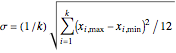 , where
, where  is the number of evaluations. The term
is the number of evaluations. The term  is the variance of a continuous uniform distribution with a domain from
is the variance of a continuous uniform distribution with a domain from 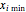 to
to  .
.
The number of Monte Carlo random trials  , the seed value, and the
, the seed value, and the 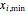 and
and  are entered with sliders. The evaluations are activated by clicking a checkbox, as is the use of the entered seed's value. In order to produce new random trials with exactly the same parameter settings, first click the "clear" button and then the "generate" button.
are entered with sliders. The evaluations are activated by clicking a checkbox, as is the use of the entered seed's value. In order to produce new random trials with exactly the same parameter settings, first click the "clear" button and then the "generate" button.
The output includes the mean and standard deviation values calculated by the above two methods, the histogram of the values generated by the Monte Carlo simulations, and a plot of the normal distribution that has the same mean and standard deviation as the generated data.
When all the  are equal to their corresponding
are equal to their corresponding  , this is equivalent to the traditional magnitude estimation method. The histogram in this case consists of a single bin, and the standard deviation value is to be printed in red.
, this is equivalent to the traditional magnitude estimation method. The histogram in this case consists of a single bin, and the standard deviation value is to be printed in red.
Permanent Citation