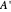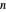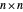Making Patterns with Wang Tiles
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
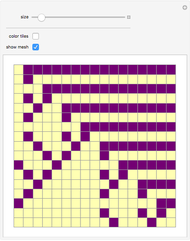
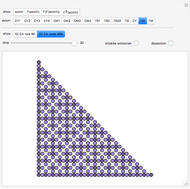
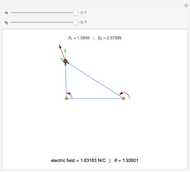
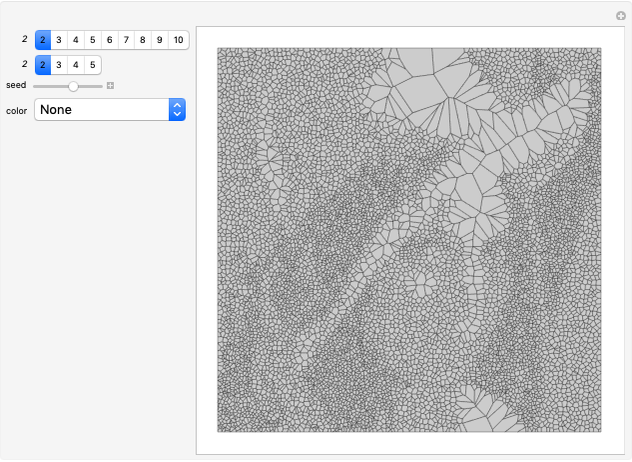
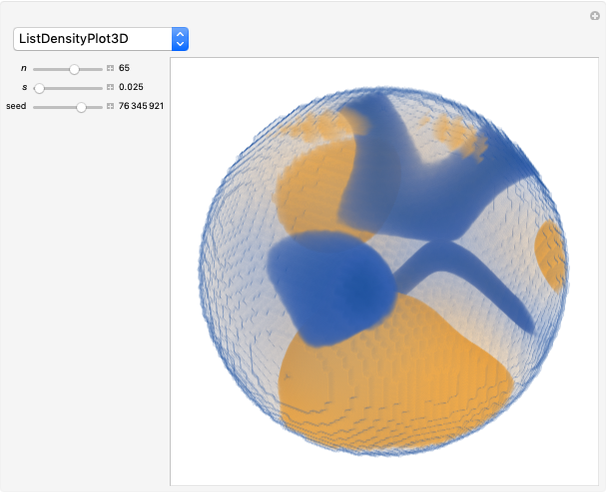
Wang tiles (constructed in 1961 by Hao Wang) are a set of 13 squares with the diagonals of each square dividing it into four colored triangles.
[more]
Contributed by: Enrique Zeleny (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Permanent Citation