Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dirac Matrices in Higher Dimensions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

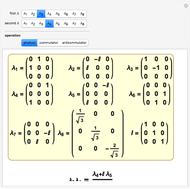
It is possible to define Dirac matrices for dimensions higher than four using Kronecker products of Pauli matrices. For dimension , there are Dirac matrices, and the dimension of the matrices is .

Contributed by: Enrique Zeleny (August 2008)
Open content licensed under CC BY-NC-SA

Details

A. Pais, "On Spinors in n Dimensions," Journal of Mathematical Physics, 3(6), 1962.

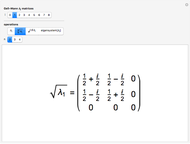
Starting with Pauli matrices , , , with , define

,

,

,

where .

For odd dimensions, the additional generator (a generalization of ) is

.

The Dirac matrices satisfy canonical anti-commutation relation .

The above definition corresponds to the so-called "chiral basis," where Dirac matrices are block anti-diagonal. Other bases are possible, and are related to the chiral basis by rotations.

The Dirac matrices generate Euclidean Clifford algebra.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send