Linearized Solution for a Mass Attached to Two Springs
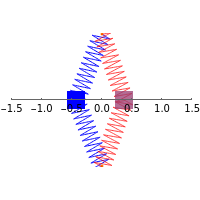
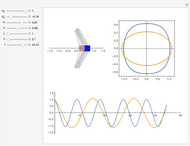
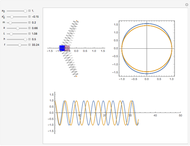
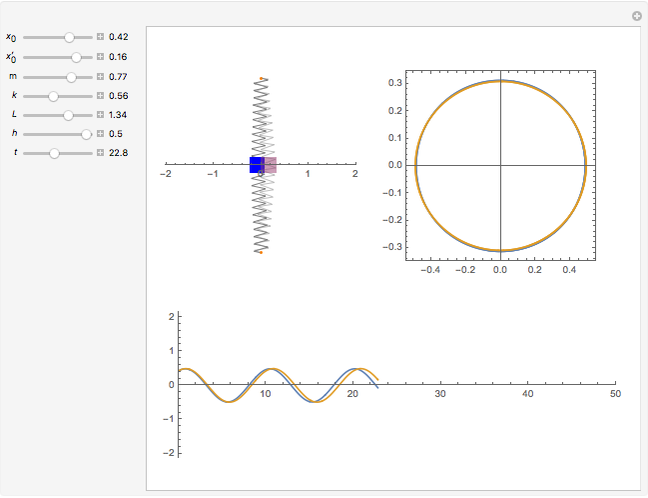
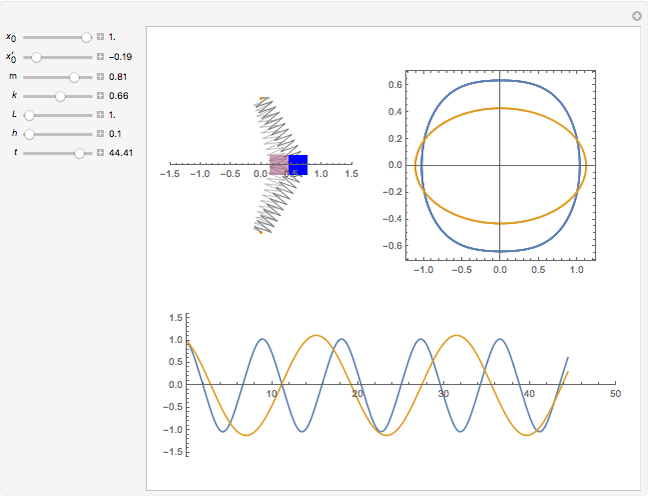
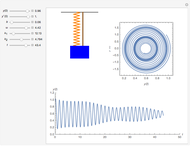
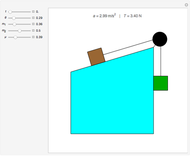
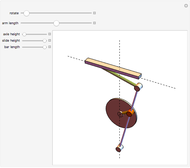
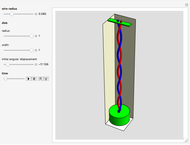
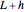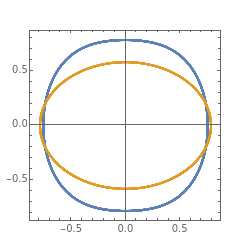
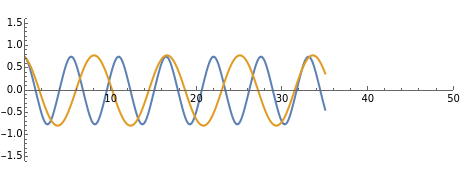
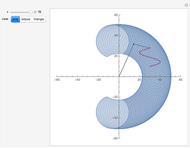
This simple nonlinear system is composed of a mass attached to two identical springs with spring constant . The lengths of the springs are in the equilibrium position and under tension. The mass is restricted to move in the direction without damping. The blue and red curves are plots of the solution of the nonlinear equation and its linearization, respectively. You can see in which cases the linearized version is a good approximation.
An equation of the type can be linearized by including just the first-order term of Taylor's expansion for 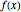to give 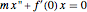. In this case, the equation of motion reduces to
and the linearized solution is
.
Reference
[1] J. R. Brannan and W. E. Boyce, Differential Equations: An Introduction to Modern Methods and Applications, 2nd ed., New York: Wiley, 2011 pp. 297–299.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
