Maximizing the Volume of a Cup Made from a Square Sheet of Paper III

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
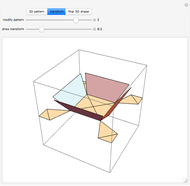
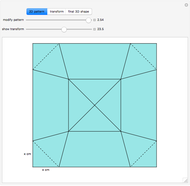
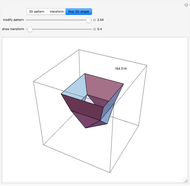
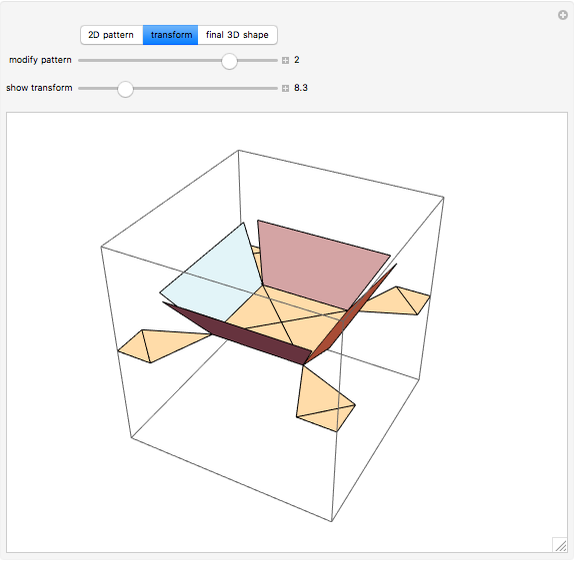
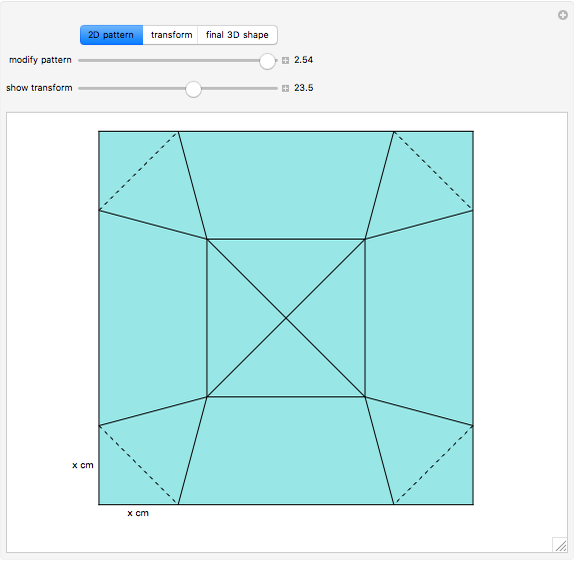
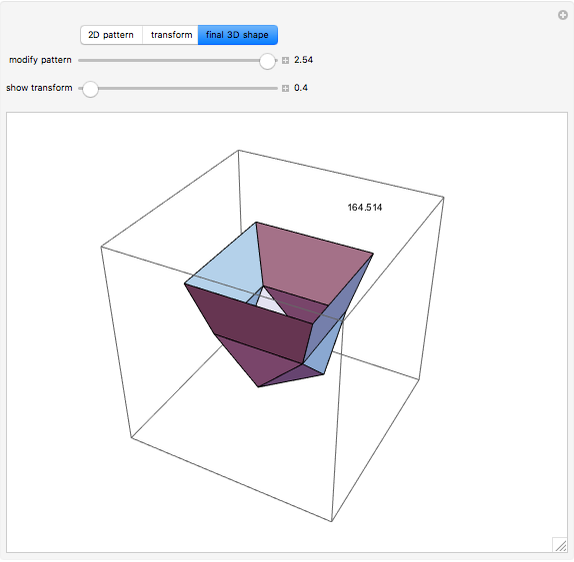
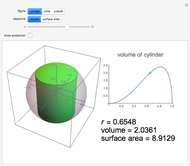
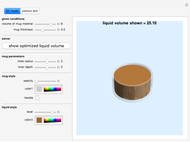
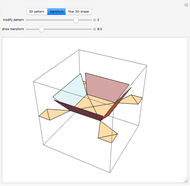
This Demonstration studies the maximization of the volume of a cup made from a square sheet of paper of size 12×12 cm. This is a new problem of mathematical origami presented by the authors [1].
Contributed by: Wataru Ogasa, Shunsuke Nakamura, and Ryohei Miyadera (January 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is not difficult to see that 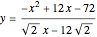 , and we can express the volume of this 3D figure with
, and we can express the volume of this 3D figure with  . The volume is
. The volume is
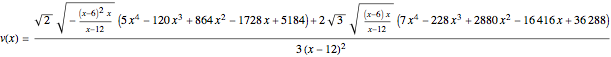 ,
,
where 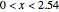 . This inequality is needed to construct the 3D figure.
. This inequality is needed to construct the 3D figure.
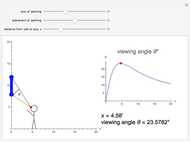
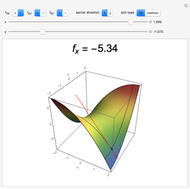
We look for the maximum value of 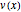 by mi=NSolve[D[v[x],x]==0,x]//Last;v[x]/.mi and we get
by mi=NSolve[D[v[x],x]==0,x]//Last;v[x]/.mi and we get 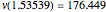 .
.
Maximizing the volume of a cup made from a square sheet of paper by using rotations is a problem proposed by the authors. Our previous research is presented in [2]. The origami wrapping problem, which has been studied by some mathematicians, looks for the biggest object that can be wrapped with a sheet of paper (see [1]).
References
[1] M. L. Catalano-Johnson and D. Loeb, "Problem 10716: A Cubical Gift," American Mathematical Monthly, 108(1), 2001 pp. 81–82.
[2] W. Ogasa, T. Inoue, K. Nishimura, T. Nakaoka, D. Ikeda, A. Kanno, S. Nakamura, H. Matsui, T. Yamauchi, S. Utsuki, and R. Miyadera, "The Maximization of a Cup Made from a Square Sheet of Paper," Science of Origami, 1(1), 2011, in Japanese.
Permanent Citation