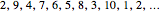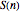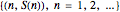Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bidirectional Variant of Josephus Problem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

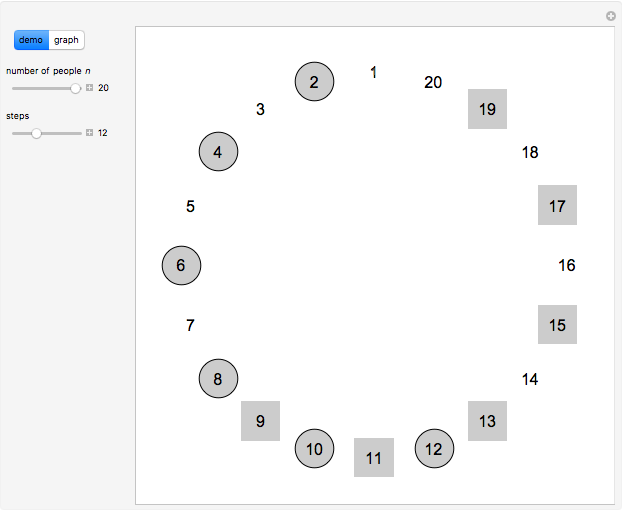
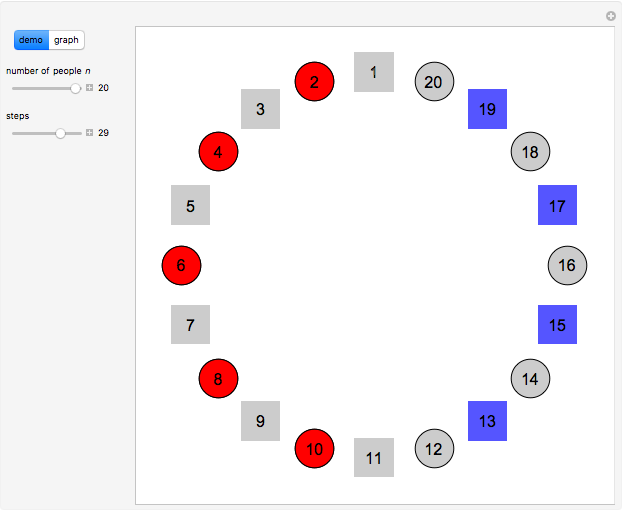
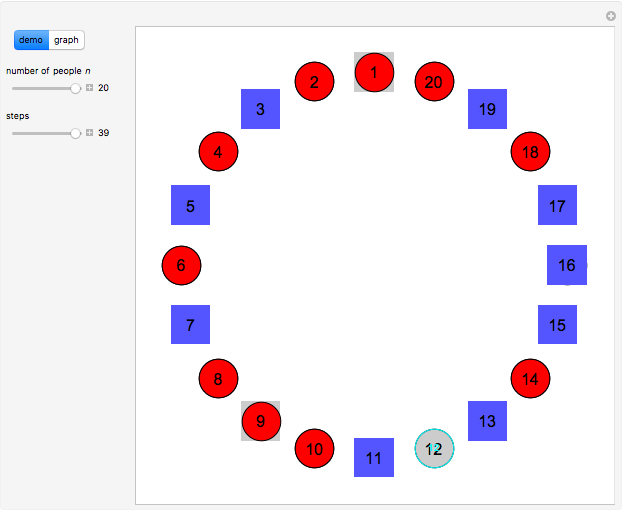
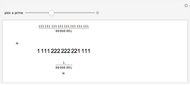
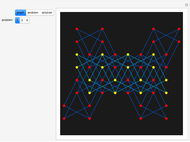
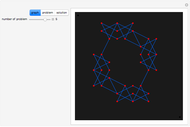
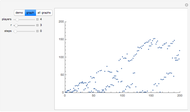
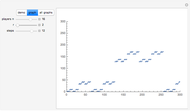
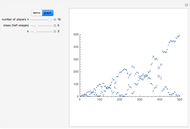
The classical version of the Josephus problem counts off people arranged in a circle and eliminates every second person. The process continues until only one person is left.

[more]

In this variant of the Josephus problem, as in the original problem, the counting is by twos. However, people are counted off alternately in opposite directions around the circle, starting from 1. When someone is counted off twice, that person is eliminated.

For example, suppose that there are 10 people. The positions of the people counted off are at . Since 2 is counted off twice, it is eliminated and the counting continues, skipping over person 2 from now on. After a while only one person is left, the survivor.

A person is covered with a gray disk or rectangle when first counted off and covered with a red disk or blue rectangle when counted off a second time and thus eliminated.

Denote the position of the survivor by . The graph of the list is a fractal.

[less]

Contributed by: Masakazu Naito and Ryohei Miyadera (September 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This new Josephus problem generalizes [1].

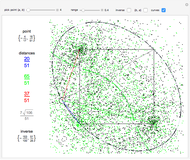
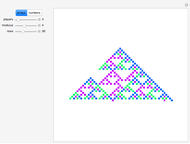
The graph of the list 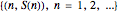is self-similar (a fractal).

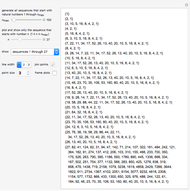
The list 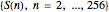 {1, 3, 4, 3, 6, 3, 3, 3, 1, 7, 5, 11, 7, 15, 14, 15, 12, 3, 12, 11, 14, 3, 22, 23, 20, 7, 28, 11, 30, 15, 11, 11, 9, 27, 5, 11, 7, 27, 3, 3, 1, 23, 5, 27, 7, 31, 19, 19, 17, 43, 13, 43, 15, 43, 27, 27, 25, 55, 29, 59, 31, 63, 54, 55, 52, 19, 52, 59, 54, 19, 46, 47, 44, 7, 52, 11, 54, 15, 46, 47, 44, 3, 44, 43, 46, 3, 54, 55, 52, 7, 60, 11, 62, 15, 86, 87, 84, 35, 84, 91, 86, 35, 78, 79, 76, 23, 84, 27, 86, 31, 110, 111, 108, 51, 108, 43, 110, 51, 118, 119, 116, 55, 124, 59, 126, 63, 43, 43, 41, 107, 37, 43, 39, 107, 35, 35, 33, 103, 37, 107, 39, 111, 19, 19, 17, 91, 13, 43, 15, 91, 27, 27, 25, 103, 29, 107, 31, 111, 11, 11, 9, 91, 5, 11, 7, 91, 3, 3, 1, 87, 5, 91, 7, 95, 19, 19, 17, 107, 13, 107, 15, 107, 27, 27, 25, 119, 29, 123, 31, 127, 75, 75, 73, 171, 69, 75, 71, 171, 67, 67, 65, 167, 69, 171, 71, 175, 51, 51, 49, 155, 45, 171, 47, 155, 59, 59, 57, 167, 61, 171, 63, 175, 107, 107, 105, 219, 101, 107, 103, 219, 99, 99, 97, 215, 101, 219, 103, 223, 115, 115, 113, 235, 109, 235, 111, 235, 123, 123, 121, 247, 125, 251, 127, 255, 214}.

If we divide these numbers by two, then the remainders are

{1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0}.

This sequence can be divided into subsequences

{1,1}, {0,1,0,1}, {1,1,1,1,1,1,1,1}, {0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1}, {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}, ,

The lengths of these subsequences are 2, 4, 8, 16, 32, .

Reference

[1] H. Matsui, T. Yamauchi, D. Minematsu, S. Tatsumi, M. Naito, T. Inoue and R. Miyadera. "The Josephus Problem in Both Directions" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheJosephusProblemInBothDirections.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send