Wolfram Demonstrations Project

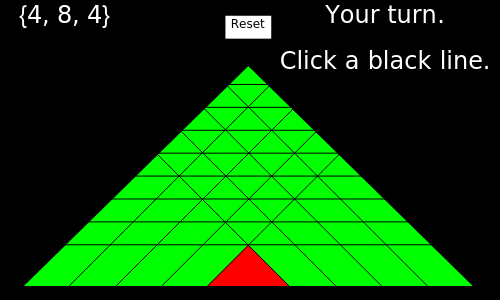
In a piece of chocolate the green parts are sweet and the red part is very bitter. This game is played by two players taking turns. Each player breaks the chocolate (in a straight line along the grooves) and eats the piece broken off. The player to leave the opponent with the single bitter part is the winner.

Contributed by: Taishi Inoue, Takuma Nakaoka, and Ryohei Miyadera

You can cut the chocolate in three ways: (1) from the upper right to the lower left, (2) horizontally, or (3) from the upper left to the lower right. Therefore it is appropriate to represent the game state with three non-negative integers

, which are shown in the upper-left corner. It is easy to see that the coordinates satisfy the inequality

We define two important states: (a)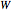

states, from which we can force a win, as long as we play correctly at every stage, and (b)

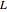states, from which we will lose however well we play if our opponent plays correctly.

One of the most important tasks of chocolate games is to find all the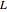

and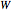

states of a game. Usually the number of

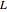states is small.

In this chocolate game it is easy to find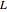

states, since there are formulas for them:
1. The position

is an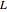

state if and only if

.
2. The position

is an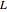

state if and only if

, where 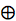⊕ is the bitwise exclusive or operation (the same as BitXor in Mathematica).

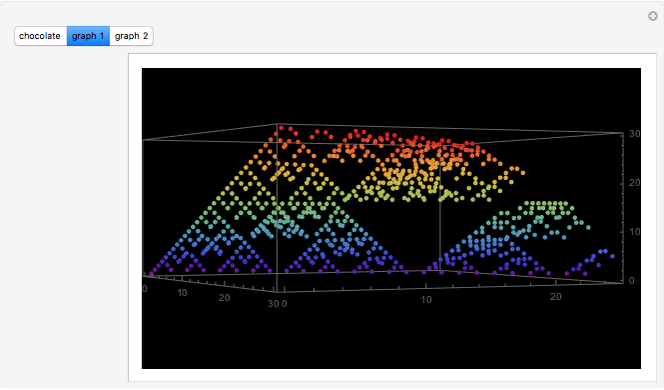
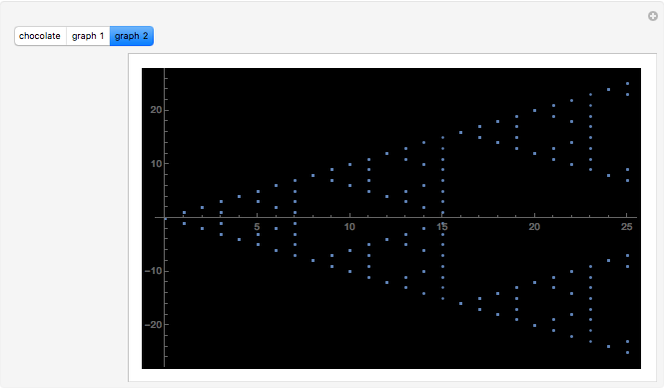
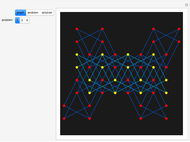
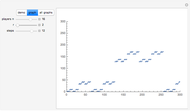
The list of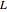

states makes a beautiful 3D graph. See "graph 1" in the Demonstration. If you rotate the graph around the

axis by

and project the list onto the plane made by the

axis and the

axis, then you get a Sierpinski gasket; see "graph 2".

Once we know the formula for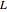

states, the strategy to win is clear. Suppose that you have a

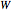state; you can choose a move that leads to an

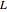state. After that any move by your opponent leads to a

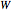state, and you can always move to an

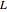state. Finally you reach

If you have to play with an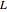

state, you can only win if your opponent makes a mistake.

See [1, 2] by the authors for a proof of the formula.

References

[1] M. Naito, T. Yamauchi, H. Matsui, T. Inoue, Y. Tomari, K. Nishimura, T. Nakaoka, D. Minematsu, and R. Miyadera, "Combinatorial Games and Beautiful Graphs Produced by Them," Visual Mathematics, 11(3), 2009. http://vismath.tripod.com/pap.htm# n114.

[2] T. Yamauchi, T. Inoue, and Y. Tomari, "Variants of the Game of Nim That Have Inequalities as Conditions," Rose–Hulman Undergraduate Mathematics Journal, 10(2), 2009. http://www.rose-hulman.edu/mathjournal/v10n2.php.