Maximizing the Volume of a Cup Made from a Square Sheet of Paper ll

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
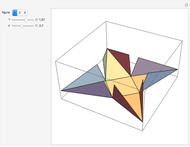
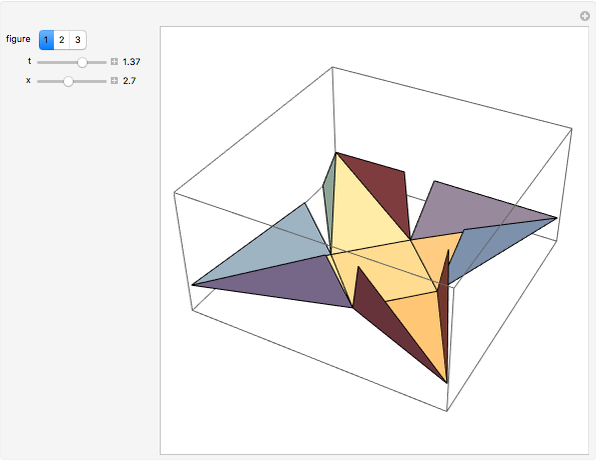
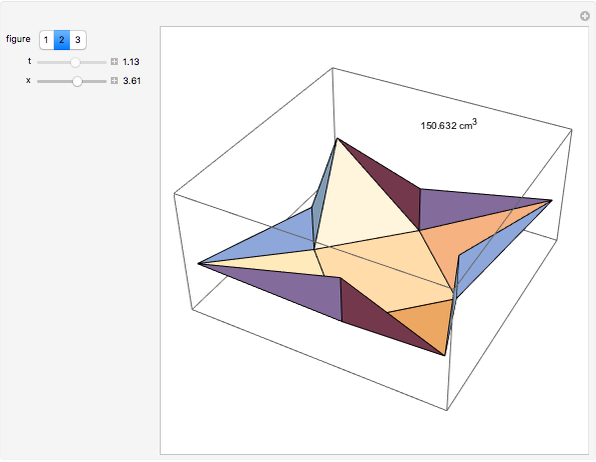
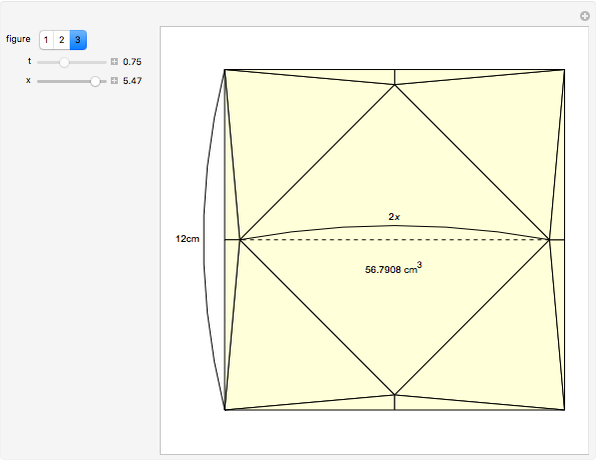
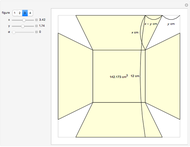
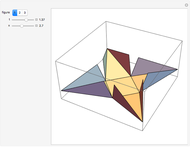
This Demonstration studies the maximization of the volume of a cup made from a square sheet of paper of size 12×12 cm. This is a new problem of mathematical origami presented by the authors.
Contributed by: Wataru Ogasa, Yuki Tomari, and Ryohei Miyadera (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
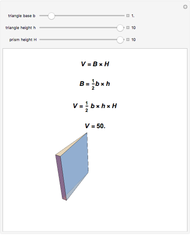
The volume of this 3D figure is 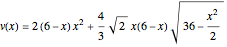 . We look for the maximum value of
. We look for the maximum value of 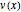 for
for 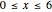 . By
. By 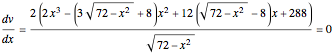 , we get
, we get 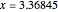 as an approximate solution and
as an approximate solution and 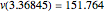 .
.
According to the referee of the Journal Origami Society of Japan, maximizing the volume of a cup made from a square sheet of paper is a new problem proposed by the authors. Our previous research is presented in [2].
The origami wrapping problem, which has been studied by some mathematicians, looks for the biggest object that can be wrapped with a sheet of paper. See [1].
References
[1] M. L. Catalano-Johnson and D. Loeb, "Problem 10716: A Cubical Gift," American Mathematical Monthly, 108(1), 2001 pp. 81–82.
[2] W. Ogasa, T. Inoue, K. Nishimura, T. Nakaoka, D. Ikeda, A. Kanno, S. Nakamura, H. Matsui, T. Yamauchi, S. Utsuki, and R. Miyadera, "The Maximization of a Cup Made from a Square Sheet of Paper," Science of Origami, 1(1), 2011, in Japanese.