Mertens Conjecture

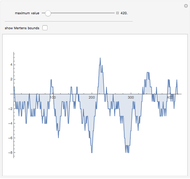
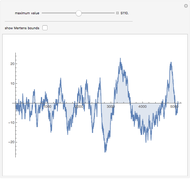
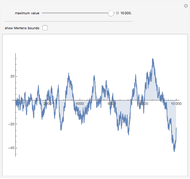
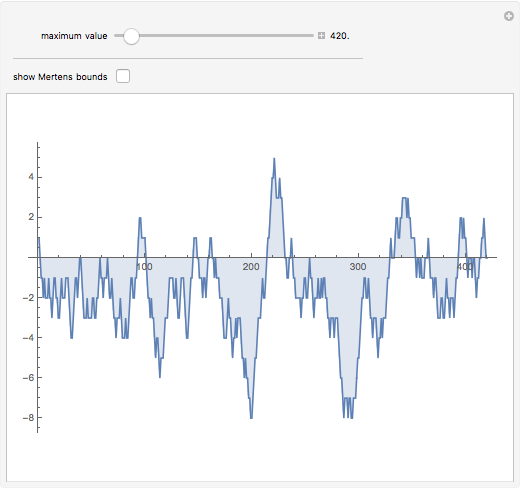
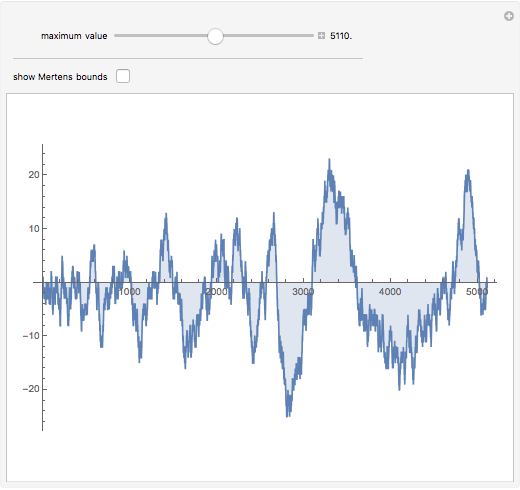
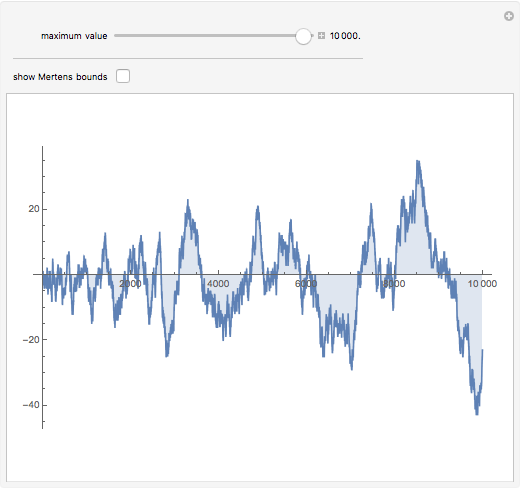
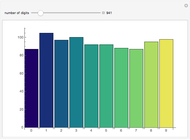
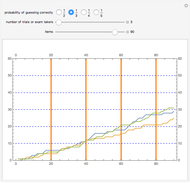
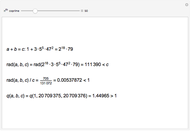
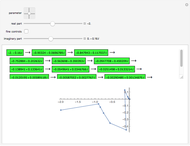
Cumulative sums of the Möbius mu function—which is essentially the parity of the number of factors in an integer, or zero if factors are repeated—follow an approximation to a random walk. The Mertens Conjecture from 1897 stated that this walk would always stay within But in 1985 it was proved that this is not so—although it is not known at what value of the first exception occurs.