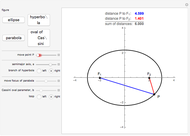
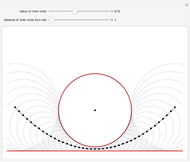
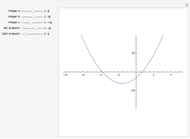
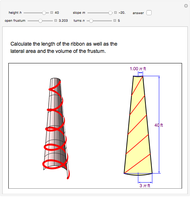
Parabola as a Locus of Centers of Circles
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
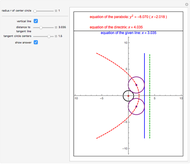
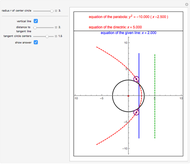
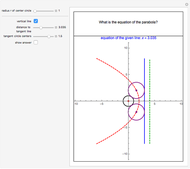
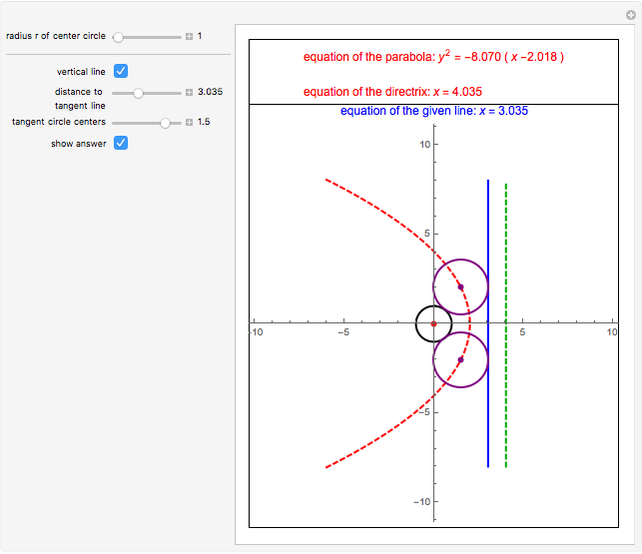
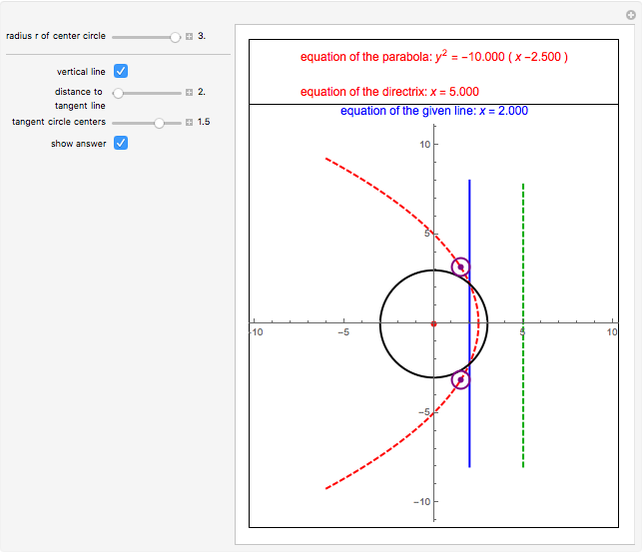
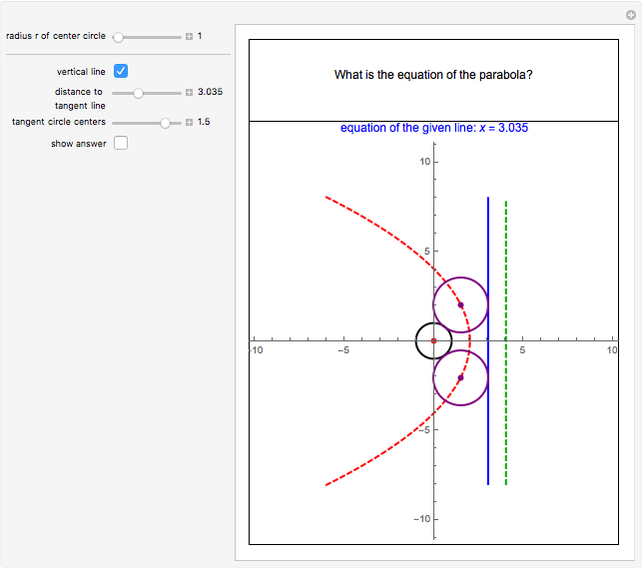
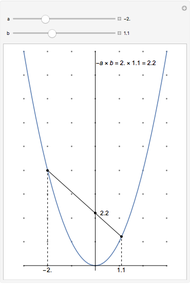
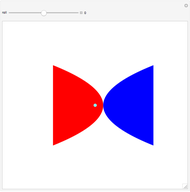
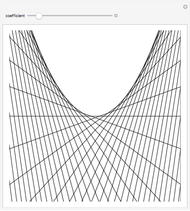
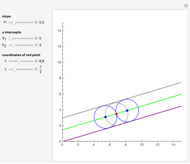
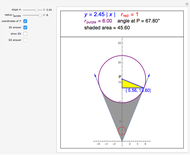
A parabola is the set of all the points that are equidistant from a fixed point  (the focus, red point) and a fixed line
(the focus, red point) and a fixed line  (the directrix, dashed green line).
(the directrix, dashed green line).
Contributed by: Abraham Gadalla (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this Demonstration,  is the origin
is the origin 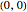 .
.
Let  be the distance from
be the distance from  to
to 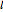 and
and  be the radius of
be the radius of 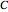 . If
. If 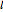 is vertical, then the equation of the parabola is
is vertical, then the equation of the parabola is  , where
, where 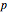 is the focal distance
is the focal distance 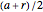 .
.
Permanent Citation