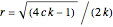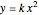Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Moving a Circle in a Parabola

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

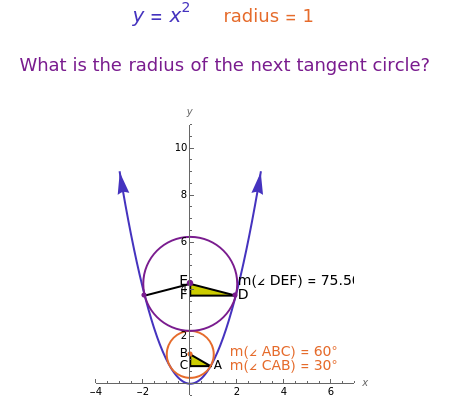
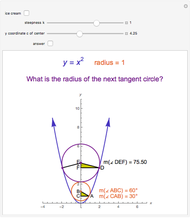
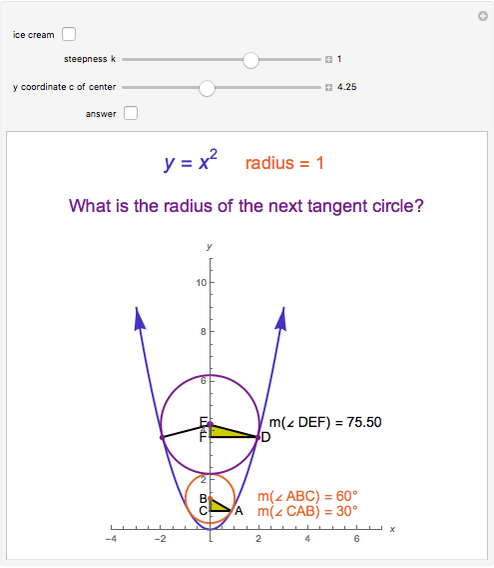
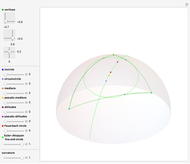
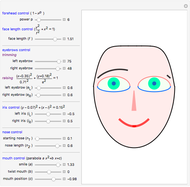
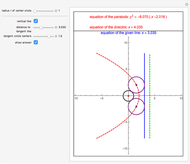
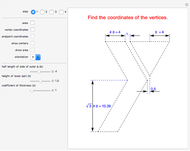
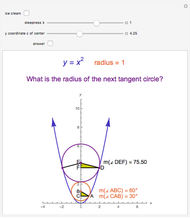
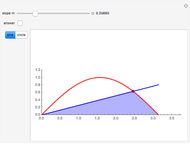
This Demonstration shows that the center 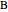of a unit circle tangent to the parabola 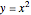is at (0, 5/4). In addition, the segment connecting the point 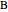and the tangent point 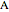makes a 60° angle with the vertical axes of the parabola.

[more]

The radius of the tangent circle with center on the axis at is , where is the steepness of the parabola .

[less]

Contributed by: Abraham Gadalla (July 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

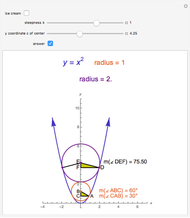
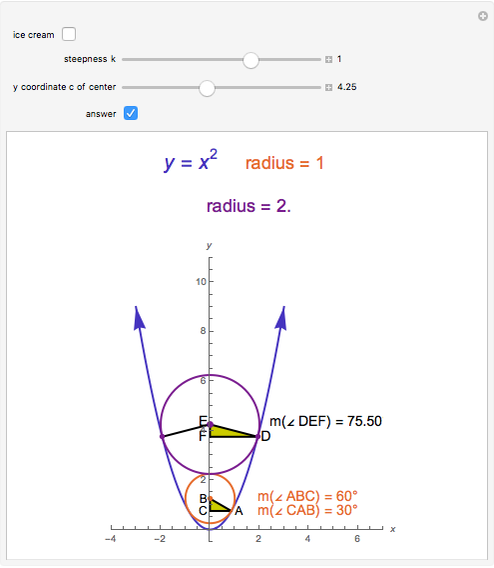
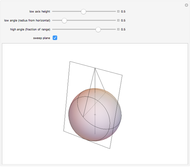
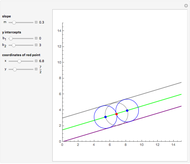
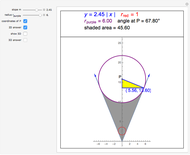
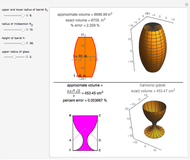
Checking the "answer" checkbox gives the radius of the purple circle. When the circles are tangent, the values of the radii are 1, 2, 3, 4, ….

Checking the "ice cream" checkbox shows the three tangent spheres and the ratio of their volumes to the volume of the paraboloid obtained by revolving 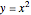about the 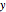axis.

Reference

[1] J. Stewart, Calculus: Early Transcendentals, 5th ed., Belmont, CA: Brooks/Cole, 2007, Chapter 3.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send