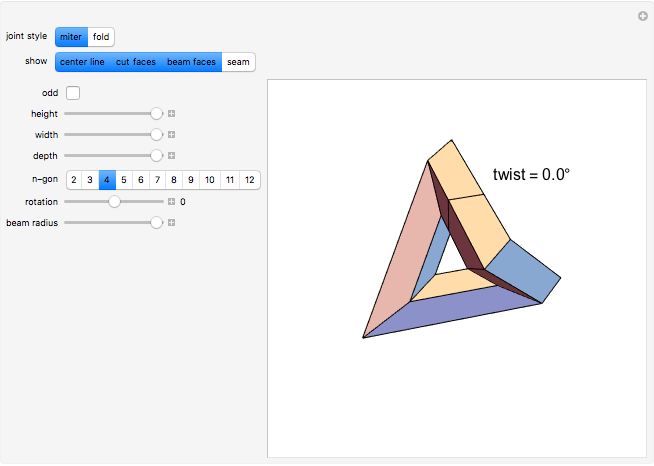
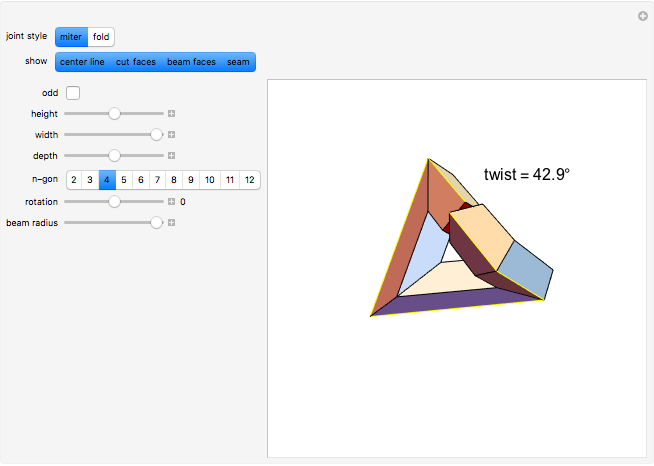
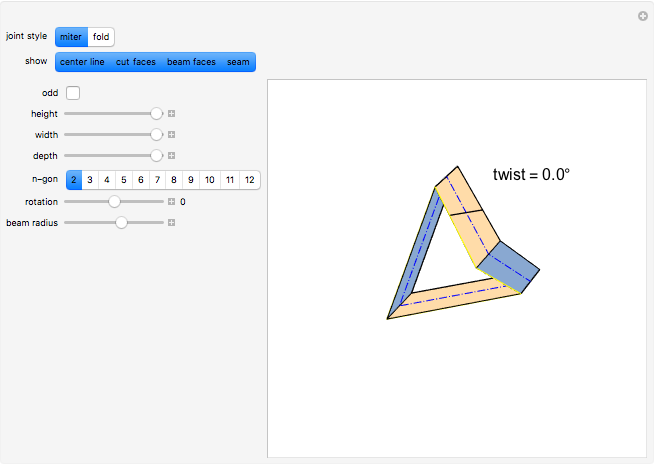
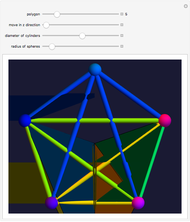
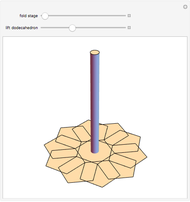
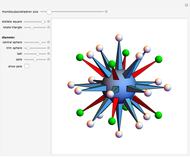
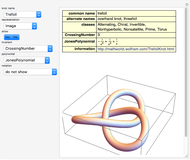
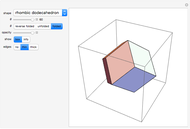
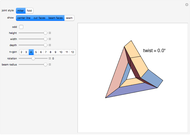
This Demonstration shows the amount of twist (writhe) that occurs when a closed 3D path is constructed from a beam using regular miter or fold joints at the vertices. The path includes four or (when "odd" is checked) five vertices of a cuboid. All beams have the same (selectable) polygonal cross section. The top beam is cut in the middle, so that the two halves can rotate with respect to each other. The height, width, and depth of the cuboid, as well as the longitudinal rotation of the beam and the beam radius, can be manipulated to see how that influences the amount of twist.
Contributed by: Tom Verhoeff (Eindhoven University of Technology)
When constructing a path in space by mitering together beams of the same cross section, it is not always the case that the edges nicely match up all the way around. Snapshot 1 shows a situation where the edges do match up. In Snapshot 2, the path is slightly altered by reducing its height and depth, resulting in a mismatch. Rotating the cross section is to no avail, as shown in Snapshot 3. The twist is more visible when highlighting a seam of the beam.
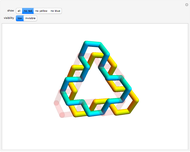
It is interesting to explore the difference between using miter joints and fold joints, in particular for an odd number of vertices. Use of a 2-gon as cross section (i.e., a strip) avoids self-intersection for fold joints. In the case of miter joints, all beams rotate in the same direction, but with fold joints adjacent, beams rotate in the opposite direction. This is illustrated in Snapshots 4 to 8.
Also see T. Verhoeff and K. Verhoeff, "The Mathematics of Mitering and Its Artful Application," in Bridges Leeuwarden: Mathematical Connections in Art, Music, and Science, Bridges 2008 Conference Proceedings (R. Sarhangi and C. Séquin, eds.), Hertfordshire, UK: Tarquin Publications, 2008. This paper presents the Miter Joint Rotation Invariance theorem, Even Fold Joint Rotation Invariance theorem, and the Odd Fold Joint Matching theorem for closed 3D paths.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_4.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_5.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_6.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_7.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_8.gif)
Embed Interactive Demonstration 
Browse all topics
