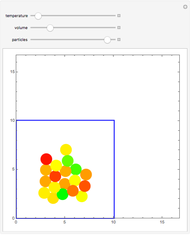
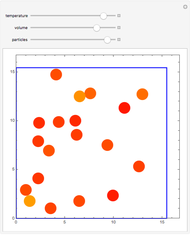
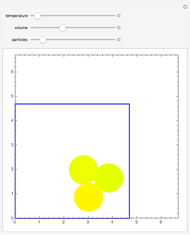
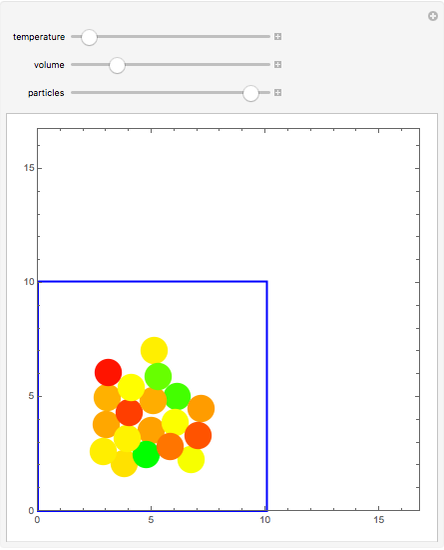
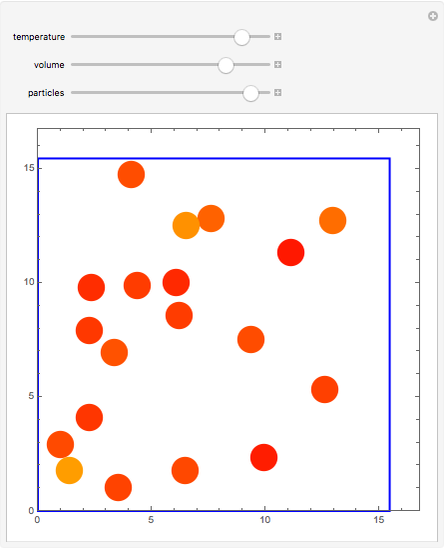
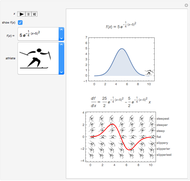
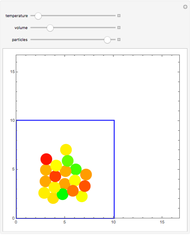
Molecular dynamics is a computer simulation technique that follows the time evolution of a set of interacting atoms or molecules by integrating their equations of motion. This Demonstration uses molecular dynamics and the velocity Verlet algorithm to simulate the motion of particles interacting under the Lennard–Jones 6-12 potential. You can vary the temperature, volume, and number of particles to change from the formation of clusters to liquid-like behavior. The color of each particle depends on its speed.