Combustion of Methane Using Block Cellular Automata (BCA) with Feedback

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
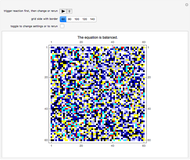
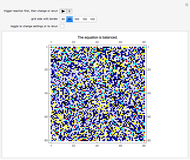
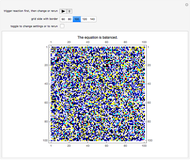
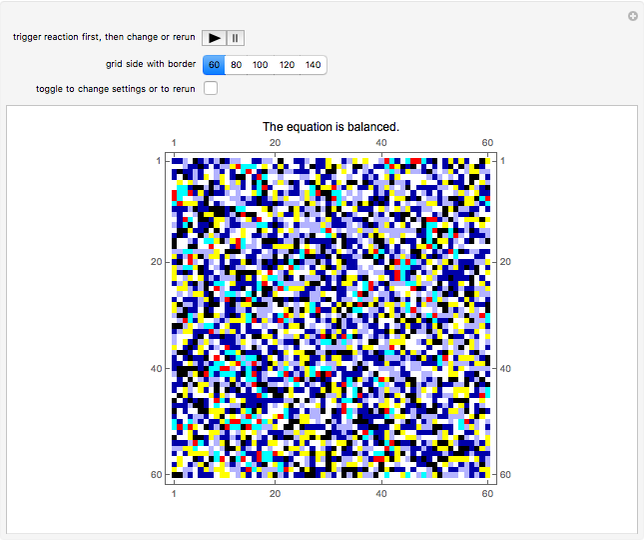
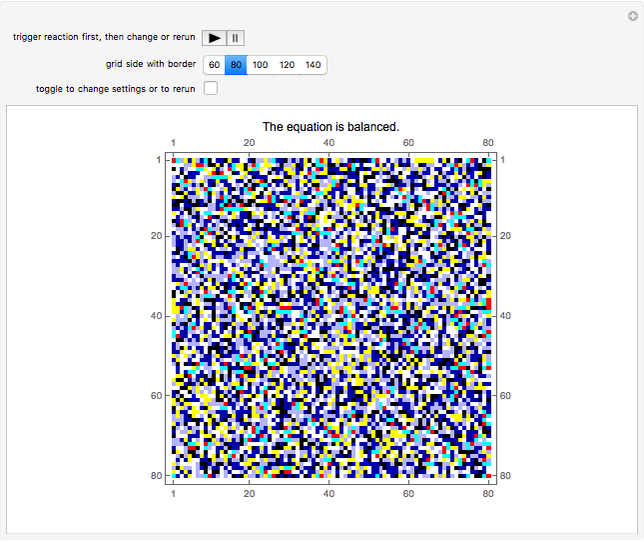
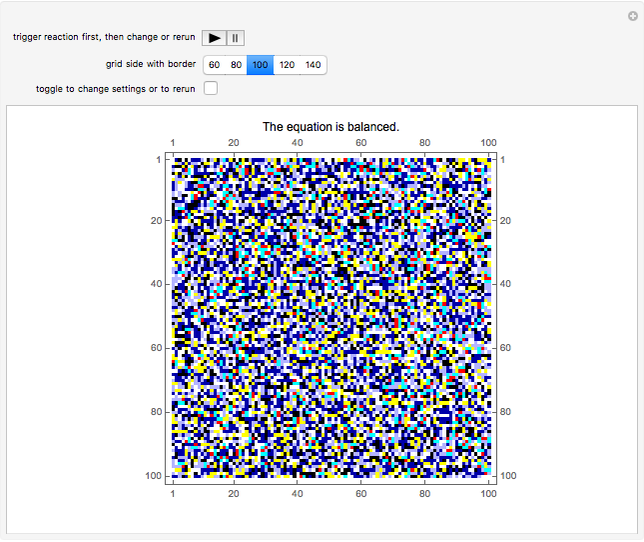
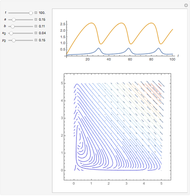
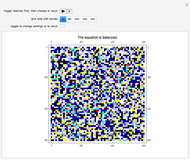
This Demonstration simulates the combustion of methane. In that reaction, the reactants 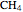 (yellow) and
(yellow) and 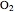 (dark blue) combine when heated to yield
(dark blue) combine when heated to yield 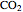 (red) and
(red) and 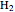 O (cyan). Carbon (black), hydrogen (white), and oxygen (pale blue) are excess constituent reactant elements also shown in the plot. The goal of the Demonstration is to demonstrate how the reaction naturally conserves matter, as reflected by the balanced equation
O (cyan). Carbon (black), hydrogen (white), and oxygen (pale blue) are excess constituent reactant elements also shown in the plot. The goal of the Demonstration is to demonstrate how the reaction naturally conserves matter, as reflected by the balanced equation 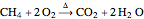 .
.
Contributed by: Michael Dewus (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Brief Chemistry Background
Conservation of matter is the basis for balancing chemical equations. Because matter is neither created nor destroyed during a chemical reaction, a balanced chemical equation must always contain the same number of each kind of atom on both sides of the equation. In this Demonstration, conservation of matter is reflected by the balanced chemical equation: 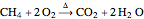 .
.
In words, the equation states that, with the application of heat, one mole of 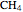 (methane) reacts with two moles of
(methane) reacts with two moles of 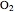 (dioxygen) to yield one mole of
(dioxygen) to yield one mole of 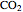 (carbon dioxide) and two moles of
(carbon dioxide) and two moles of 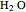 (water).
(water).
Demonstration Mechanics
At initialization, the grid is configured as a random mixture of excess carbon ( ), excess hydrogen (
), excess hydrogen (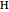 ), excess oxygen (
), excess oxygen (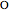 ), and the reactants
), and the reactants 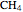 and
and 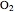 . The reactant concentrations are relative to the grid size, and are fixed at 15%
. The reactant concentrations are relative to the grid size, and are fixed at 15% 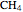 to 30%
to 30% 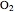 , which reflects the left-hand side of the equation.
, which reflects the left-hand side of the equation.
A feedback-driven block cellular automaton (BCA) searches the grid for 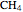 locations surrounded by exactly two
locations surrounded by exactly two 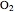 molecules and rewrites the
molecules and rewrites the 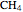 and
and 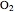 locations to
locations to 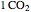 and
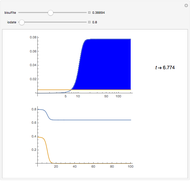
and 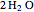 , respectively, reflecting the right-hand side of the equation. Reaction catalyzing heat is introduced through the rotational mixing energy of the BCA. As the reaction proceeds, the plot label monitors the counts of the reactants and their ratio as well as the counts of the products and their ratio in order to show a left-hand side to right-hand side balance history of the rewritten grid. Thus grid rewrite, itself a function of respective bondings, is ultimately responsible for determining whether or not the equation balances. The time to balance the equation is an indication of how much heat was necessary to bring about the balance. In keeping with the law of conservation of matter, the equation must always ultimately balance.
, respectively, reflecting the right-hand side of the equation. Reaction catalyzing heat is introduced through the rotational mixing energy of the BCA. As the reaction proceeds, the plot label monitors the counts of the reactants and their ratio as well as the counts of the products and their ratio in order to show a left-hand side to right-hand side balance history of the rewritten grid. Thus grid rewrite, itself a function of respective bondings, is ultimately responsible for determining whether or not the equation balances. The time to balance the equation is an indication of how much heat was necessary to bring about the balance. In keeping with the law of conservation of matter, the equation must always ultimately balance.
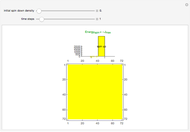
After triggering the reaction first (only once is necessary), toggle the "change settings" control to rerun the reaction with a different grid size or to rerun with a different underlying grid and current settings.
References
[1] K. W. Whitten and K. D. Gailey, General Chemistry, Philadelphia, PA: Saunders College Publishing, 1981.
[2] Wolfram|Alpha—A Wolfram Web Resource. www.wolframalpha.com.
[3] Wikipedia. "Methane." (Aug 17, 2012) en.wikipedia.org/wiki/Methane.
[4] Wikipedia. "Carbon." (Aug 12, 2012) en.wikipedia.org/wiki/Carbon.
[5] Wikipedia. "Hydrogen." (Aug 14, 2012) en.wikipedia.org/wiki/Hydrogen.
[6] Wikipedia. "Oxygen." (Aug 20, 2012) en.wikipedia.org/wiki/Oxygen.
Permanent Citation