Natural Modes of Vibrations for Some Simple Systems

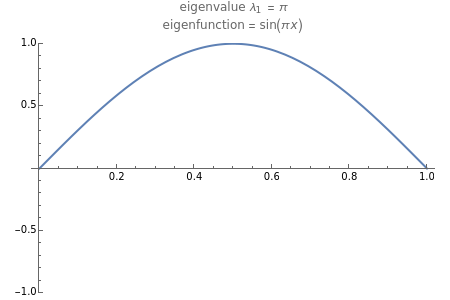
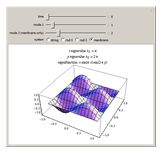
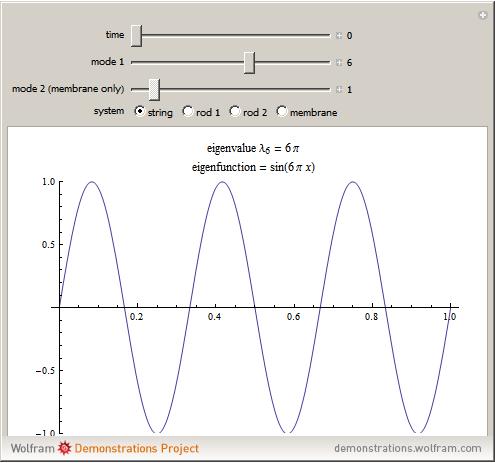
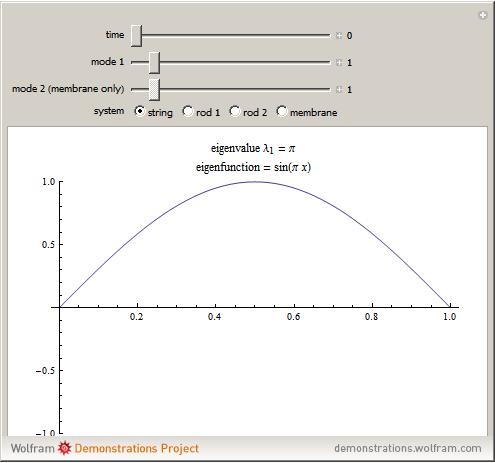
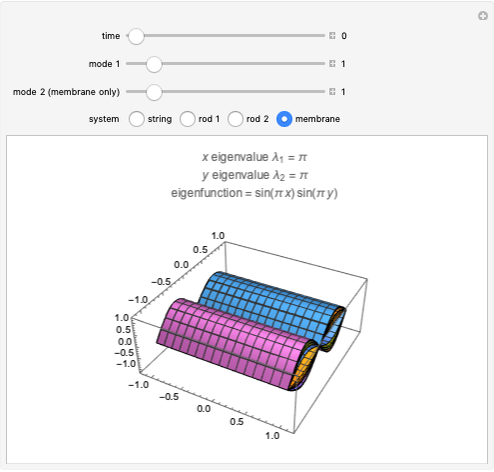
This Demonstration displays the animation of eigenmodes of some simple vibrating systems. The eigenfunctions and eigenvalues are evaluated by solving the eigenvalue
problem associated with the one- or two-dimensional wave equation. The systems considered are a fixed-fixed (left boundary condition-right boundary condition) string, fixed-fixed 1D rod, a 1D rod free at both ends, and a fixed square membrane. The rod in consideration is a 1D thin rod with no flexural bending. As the time slider moves, the evolution of the eigenmode in time is simulated using the general form of the solution to the wave equation. The sliders for mode 1 and mode 2 simulate the different eigenmodes—the first 10 modes for the system. Mode 2 is specifically for the simulation of the membrane, and is disabled for the one-dimensional systems.