Normal Oscillatory Modes of Rotating Orthotropic Disks
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
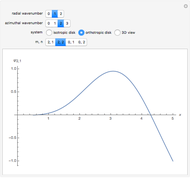
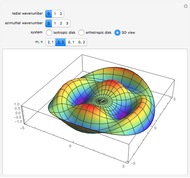
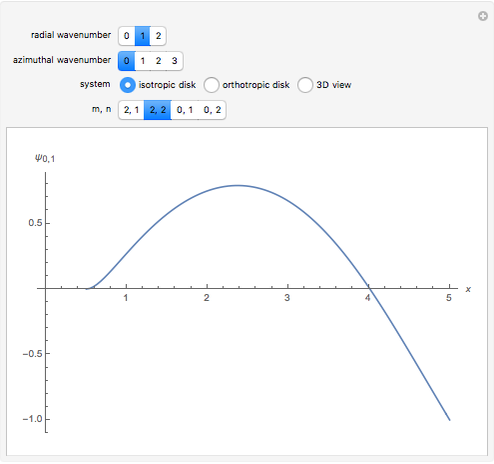
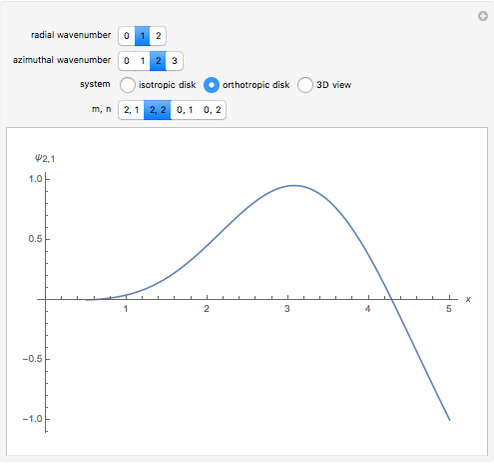
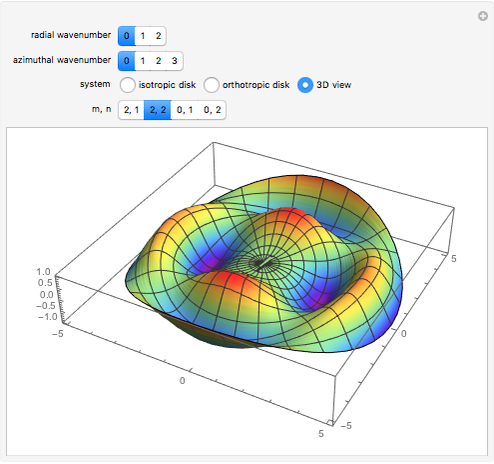
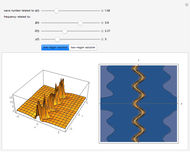
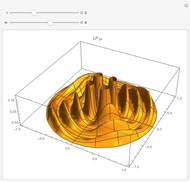
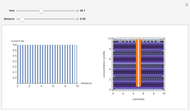
Radial eigenfunctions and mode shapes for rotating isotropic and orthotropic disks. The ratio of the outer radius to the inner radius of the disk is 10.
Contributed by: Atefeh Khoshnood and Mir Abbas Jalali (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation
"Normal Oscillatory Modes of Rotating Orthotropic Disks"
http://demonstrations.wolfram.com/NormalOscillatoryModesOfRotatingOrthotropicDisks/
Wolfram Demonstrations Project
Published: March 7 2011
Normal Modes of a Beaded String
Enrique Zeleny
Normal Modes in a Periodic Square Lattice
Luis Elcoro (University of the Basque Country, Spain)
Gaussian Laser Modes
Antoine Weis
Natural Modes of Vibrations for Some Simple Systems
Pratik Desai
Optical Rotation and Ellipticity
Jochen Autschbach
Polarization of an Optical Wave through Polarizers and Wave Plates
Fred E. Moolekamp and Kevin L. Stokes (University of New Orleans)
Optical Rogue Waves (Rogons)
Zhenya Yan
Core Intensity Profiles for Linearly Polarized Modes in Optical Fibers
John Miller
Scanning Electrochemical Microscopy in Substrate Generator/Tip Collector Mode
Quang-Dao Trinh
Normal Modes in a Periodic Monatomic Linear Chain
Luis Elcoro (University of the Basque Country, Spain)
