Normal Modes in a Periodic Square Lattice

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
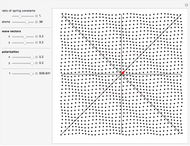
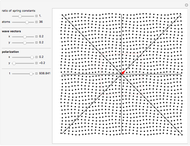
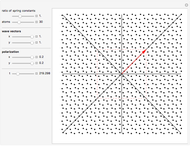
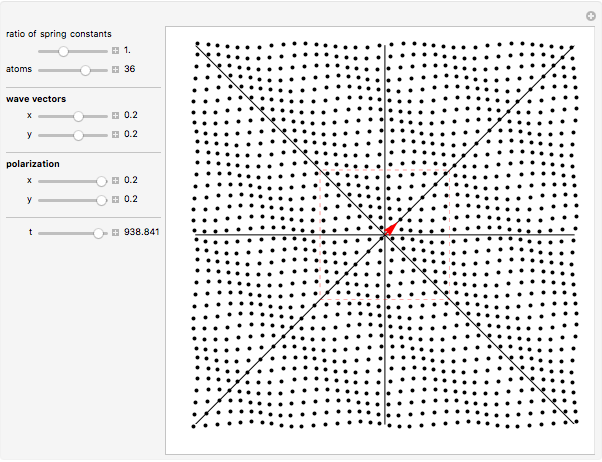
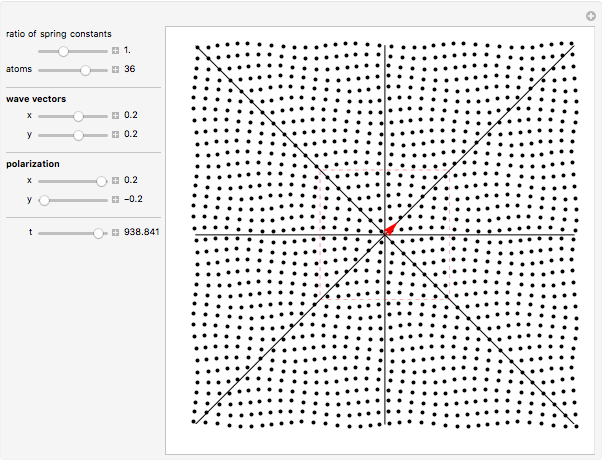
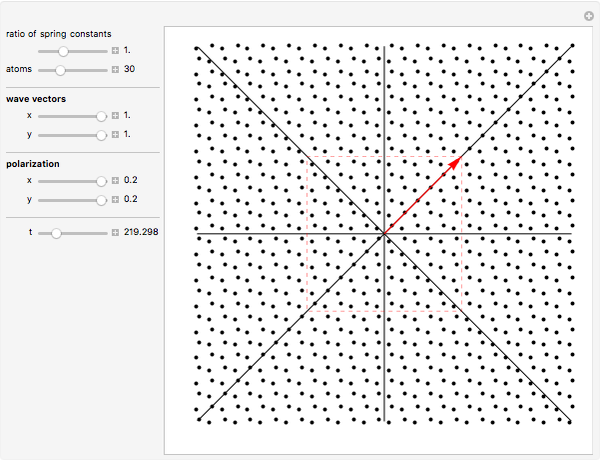
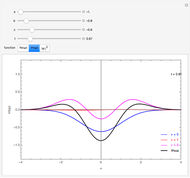
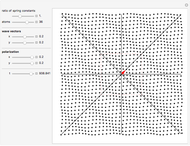
Normal modes in a monatomic periodic square chain are simulated. You can adjust the number of atoms, the ratio between the two "spring constants", the two components of the wave vector 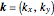 (red arrow) in the first Brillouin zone (red square), and the two components of the polarization
(red arrow) in the first Brillouin zone (red square), and the two components of the polarization 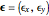 . Sound waves (small
. Sound waves (small 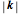 ) and stationary waves (within the boundary of the Brillouin zone) can be easily identified. Longitudinal (
) and stationary waves (within the boundary of the Brillouin zone) can be easily identified. Longitudinal ( parallel to
parallel to  ) and transverse (
) and transverse ( perpendicular to
perpendicular to  ) waves are also clearly reproduced.
) waves are also clearly reproduced.
Contributed by: Luis Elcoro (University of the Basque Country, Spain) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
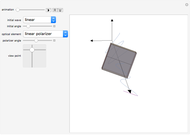
Snapshot 1: static atomic configuration for a long wavelength longitudinal normal mode
Snapshot 2: static atomic configuration for a long wavelength transverse normal mode
Snapshot 3: static atomic configuration for a normal mode with a wave vector at the boundary of the first Brillouin zone
Permanent Citation
"Normal Modes in a Periodic Square Lattice"
http://demonstrations.wolfram.com/NormalModesInAPeriodicSquareLattice/
Wolfram Demonstrations Project
Published: March 7 2011