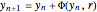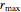Numerical Integration of the Logistic Equation Using Runge-Kutta Methods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
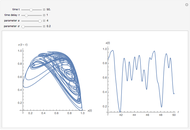
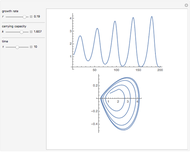
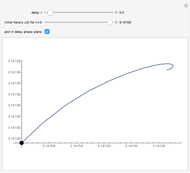
The continuous logistic model is described by the differential equation  , where
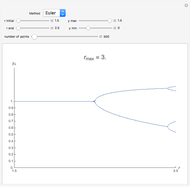
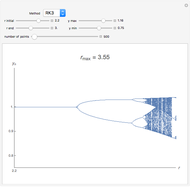
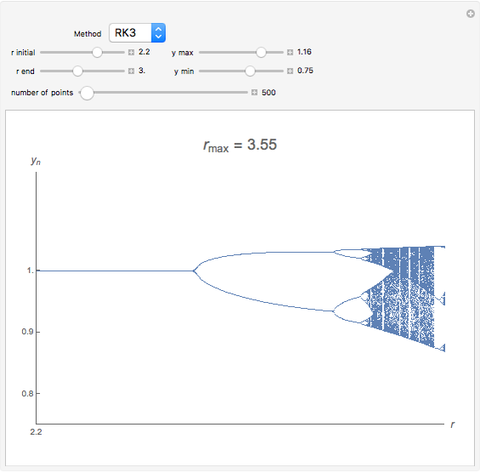
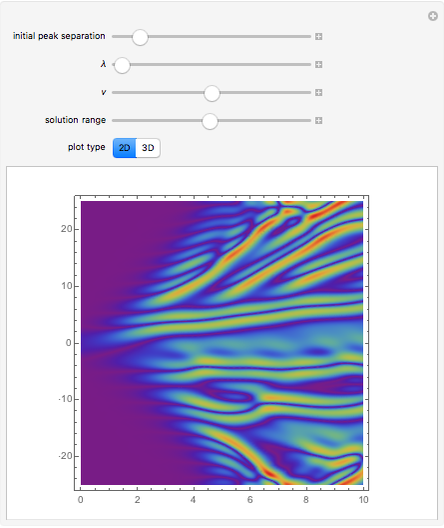
, where  is known as the Malthusian parameter. This Demonstration allows you to integrate this DE numerically with several Runge–Kutta methods with orders from 1 up to 3, with constant step size
is known as the Malthusian parameter. This Demonstration allows you to integrate this DE numerically with several Runge–Kutta methods with orders from 1 up to 3, with constant step size  and initial value
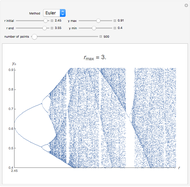
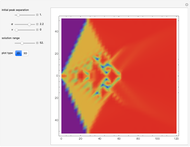
and initial value 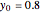 . This procedure illustrates chaos and bifurcation. In particular, by using the Euler method, the map is very similar to the classic logistic map, but other RK methods give different and more interesting maps.
. This procedure illustrates chaos and bifurcation. In particular, by using the Euler method, the map is very similar to the classic logistic map, but other RK methods give different and more interesting maps.
Contributed by: Luis Rández (January 2012)
Based on programs by: Robert M. Lurie
Open content licensed under CC BY-NC-SA
Snapshots
Details
This formulation is modified from that given in [1], p. 941 ff.
Reference
[1] H. Ruskeepää, Mathematica Navigator, 3rd ed., San Diego: Academic Press, 2009.
Permanent Citation