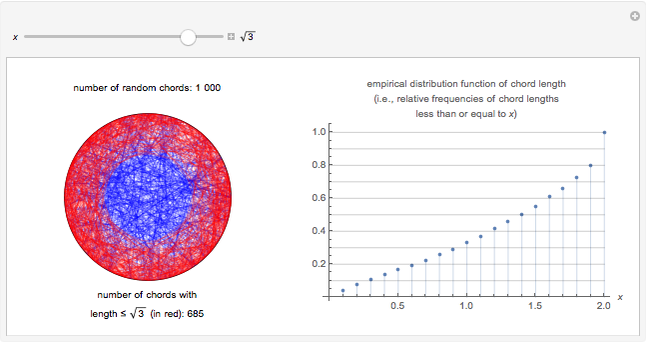
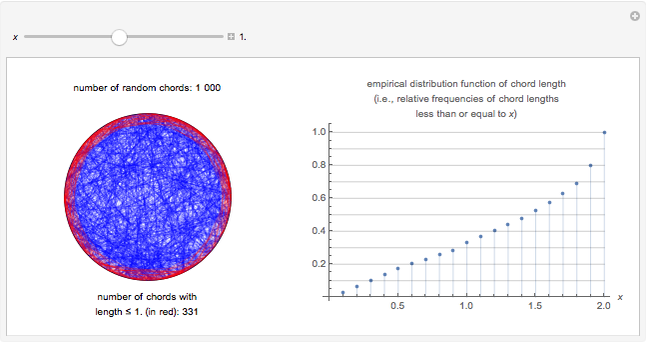
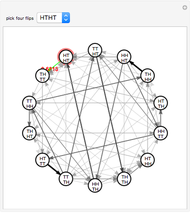
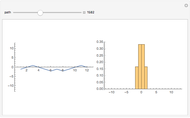
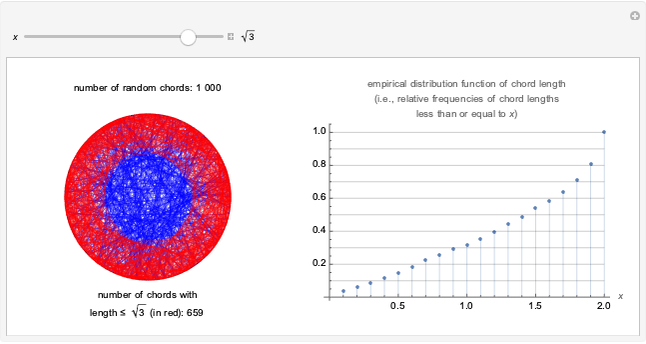
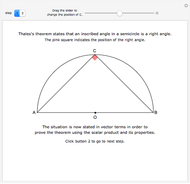
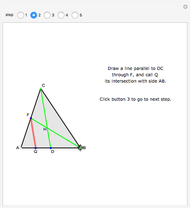
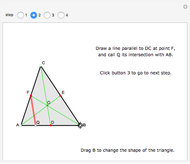
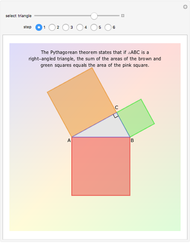
There are several possible definitions of what is meant by a random chord in a unit circle. Here, two angles are chosen at random in 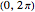, and the two corresponding points on the circumference are joined by a line, that is, a chord. Using this method, a sample of 1000 such chords is obtained and, for a given value of , the frequency of chord lengths less than or equal to is computed, giving an approximation to the probability distribution function of chord length.