Obtuse Random Triangles from Three Points in a Rectangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
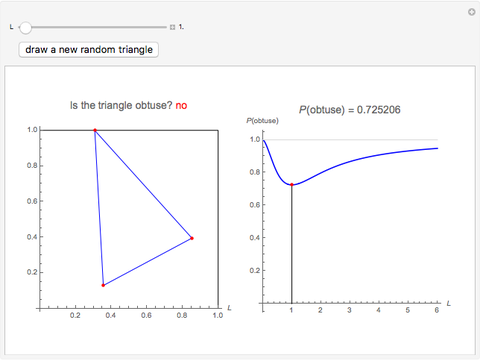
Choose three random points from the rectangle 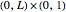 to form a triangle. What is the probability that the triangle is obtuse? This Demonstration shows random triangles and the probability as a function of
to form a triangle. What is the probability that the triangle is obtuse? This Demonstration shows random triangles and the probability as a function of 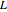 .
.
Contributed by: Heikki Ruskeepää (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
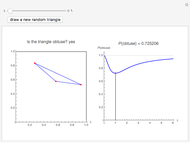
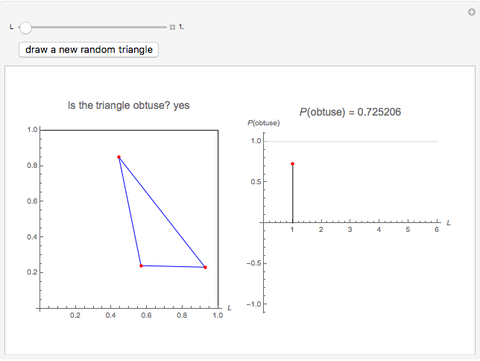
Snapshot 1: In a square, the probability that the random triangle is obtuse is at its lowest value, 0.725, but even this is quite a high value. Approximately only a quarter of the random triangles are not obtuse.
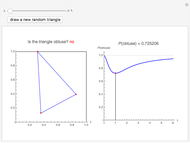
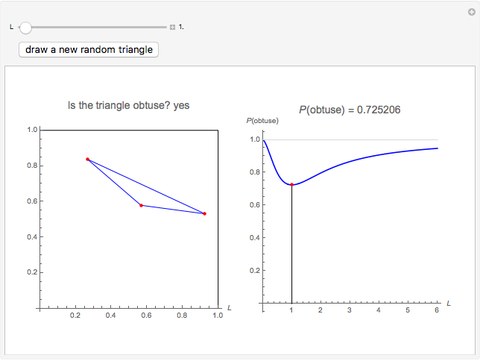
Snapshot 2: an example where a random triangle in a square is not obtuse
Snapshot 3: For narrower rectangles, the probability that the random triangle is obtuse is even higher. For a rectangle with sides 6 and 1, the probability is 0.948.
Snapshot 4: an example where a random triangle in a  rectangle is not obtuse
rectangle is not obtuse
In 1955, Frank Hawthorne [1] presented the following problem: "If three points are selected at random in a rectangle 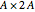 , what is the probability that the triangle so determined is obtuse?" The problem turned out to be so difficult that no solutions were obtained for 15 years.
, what is the probability that the triangle so determined is obtuse?" The problem turned out to be so difficult that no solutions were obtained for 15 years.
In 1970, Eric Langford [2] solved the problem, moreover for arbitrary rectangles: "Let there be given three points at random in an arbitrary rectangle. What is the probability that the triangle thus formed is obtuse?" The problem is also considered in Nahin [3, pp. 8–11].
Consider the rectangle 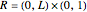 , and let
, and let 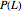 be the probability of a random triangle in
be the probability of a random triangle in  being obtuse. The solution of the problem is as follows. If
being obtuse. The solution of the problem is as follows. If  , then
, then
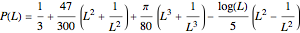 .
.
If 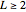 , then
, then
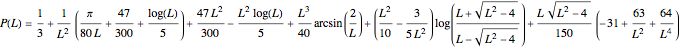 .
.
If 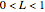 , use the relation
, use the relation 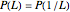 .
.
Two interesting special cases are  (the rectangle is a square) and
(the rectangle is a square) and  (Hawthorne's original problem):
(Hawthorne's original problem):
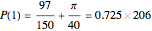 ,
,
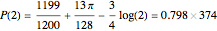 .
.
The probability that the triangle is obtuse is at its minimum for  . The probabilities are approximately 0.95, 0.99, and 0.999 when
. The probabilities are approximately 0.95, 0.99, and 0.999 when 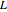 is 6.2, 17.1, and 65.3, respectively.
is 6.2, 17.1, and 65.3, respectively.
References
[1] F. Hawthorne, Problem E1150, American Mathematical Monthly, 62, 1955, p. 40.
[2] E. Langford, "A Problem in Geometric Probability," Mathematics Magazine, 40, pp. 237–244. http://www.maa.org/programs/maa-awards/writing-awards/a-problem-in-geometric-probability.
[3] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton, NJ: Princeton University Press, 2008.
Permanent Citation