Orthogonal Systems of Circles on the Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
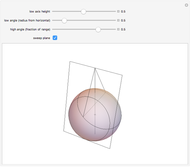
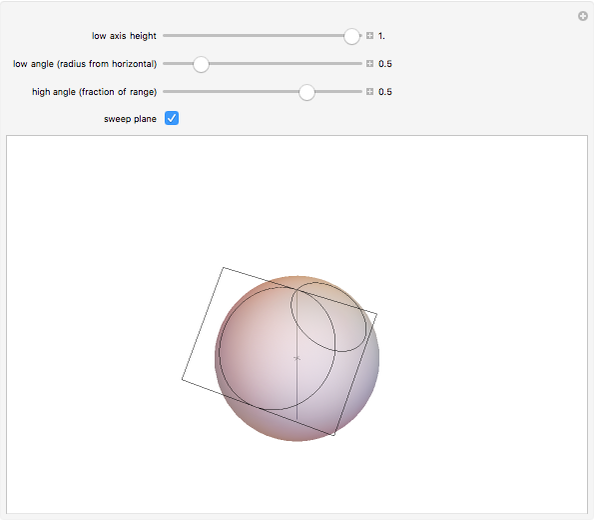
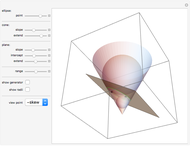
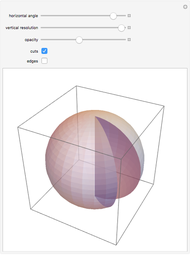
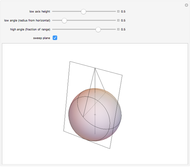
This Demonstration shows two families of circles on the sphere such that each circle in one family is orthogonal to each circle of the other family. In the plane these are called Apollonian circles.
[more]
Contributed by: Mark D. Meyerson (May 2012)
Open content licensed under CC BY-NC-SA
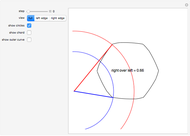
Snapshots
Details
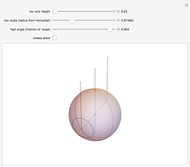
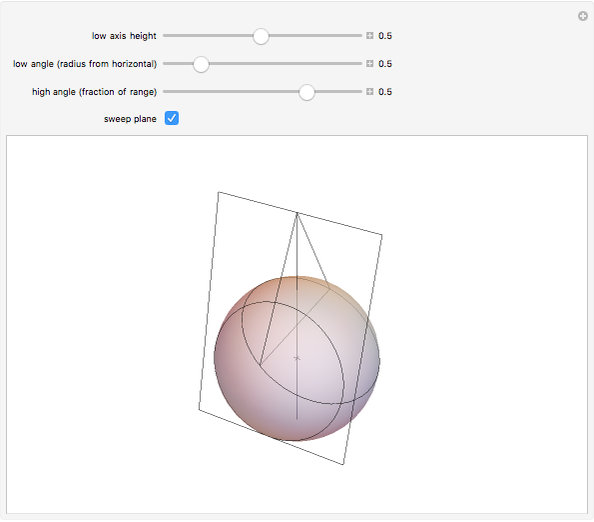
1. Assume that the sphere is centered at the origin and has unit radius. The low axis is a line parallel to the 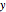 axis through the point
axis through the point 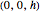 with
with  between 0 and 1. The first family of circles consists of all intersections of the sphere with planes through this line. The high axis is a line parallel to the
between 0 and 1. The first family of circles consists of all intersections of the sphere with planes through this line. The high axis is a line parallel to the  axis at a distance
axis at a distance 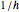 from the origin, cutting the
from the origin, cutting the  axis at
axis at 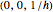 . (If
. (If  , then it is viewed as a line at infinity.) The second family of circles is given by the intersections of the sphere with planes through this line. Just as in the latitude/longitude case, with the exception of at most two points, every point of the sphere is intersected by exactly one circle from each family and the two circles are orthogonal at their intersection.
, then it is viewed as a line at infinity.) The second family of circles is given by the intersections of the sphere with planes through this line. Just as in the latitude/longitude case, with the exception of at most two points, every point of the sphere is intersected by exactly one circle from each family and the two circles are orthogonal at their intersection.
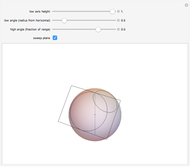
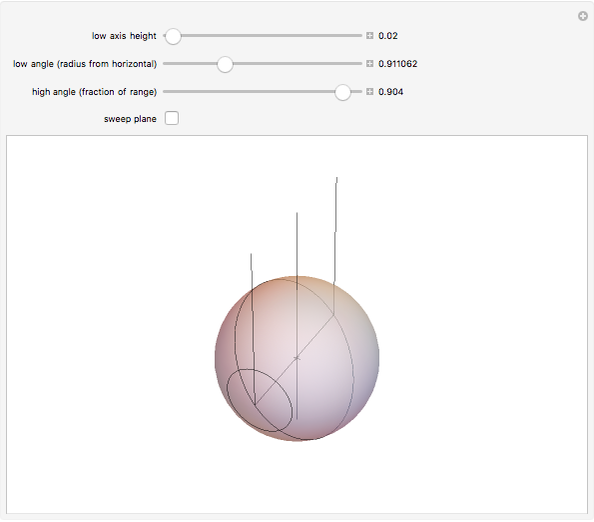
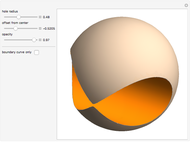
2. There are two special cases. If  , then the second axis is viewed as a line at infinity (snapshot 3). The planes through the axis are perpendicular to the
, then the second axis is viewed as a line at infinity (snapshot 3). The planes through the axis are perpendicular to the 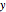 axis, and so this is our original motivating example of circles of latitude and longitude, with the
axis, and so this is our original motivating example of circles of latitude and longitude, with the 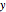 axis as the polar axis. The other extreme is when
axis as the polar axis. The other extreme is when  (snapshot 2). Then the two axes meet at
(snapshot 2). Then the two axes meet at 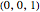 and that is the only point not on only one pair of circles.
and that is the only point not on only one pair of circles.
3. To view the orthogonality of pairs of circles through a point, drag to rotate the sphere until the intersection point lies over the center of the sphere. Then you are looking straight down onto the plane of tangency at the point of intersection so the angle appears accurate. One can prove this orthogonality with a fairly straightforward use of vectors, cross products, and dot products.
4. In the special case of  , there is an easy way to see perpendicularity. For by symmetry, circles meeting at two points form the same angle at both intersections. At
, there is an easy way to see perpendicularity. For by symmetry, circles meeting at two points form the same angle at both intersections. At 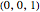 the tangents to the circles are in the direction of the
the tangents to the circles are in the direction of the  and
and 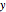 axes, and so are perpendicular. (See snapshot 2.)
axes, and so are perpendicular. (See snapshot 2.)
5. Apollonian circles in the plane can be found by stereographically projecting these spherical systems. These are also known as coaxial (or coaxal) systems of circles and lines. In particular, the  and
and  cases project to polar and rectangular coordinate systems, respectively.
cases project to polar and rectangular coordinate systems, respectively.
6. See http://en.wikipedia.org/wiki/Apollonian_circles for a discussion in the plane.
Permanent Citation