Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Pascal's Angle Trisection

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

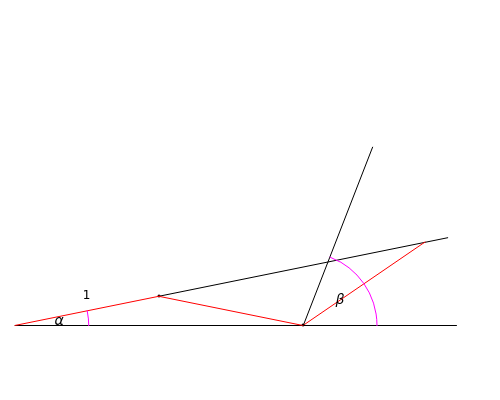
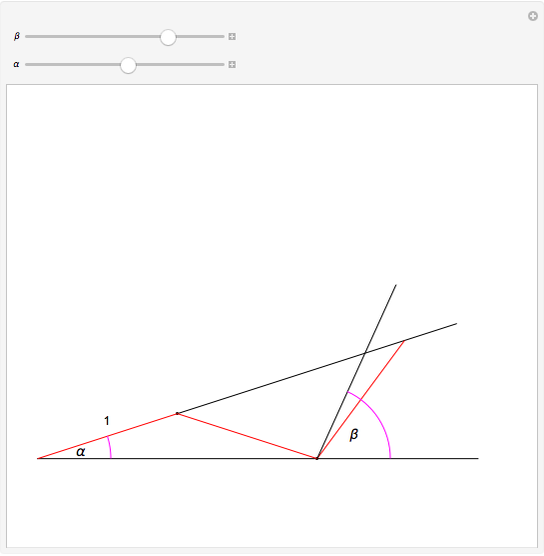
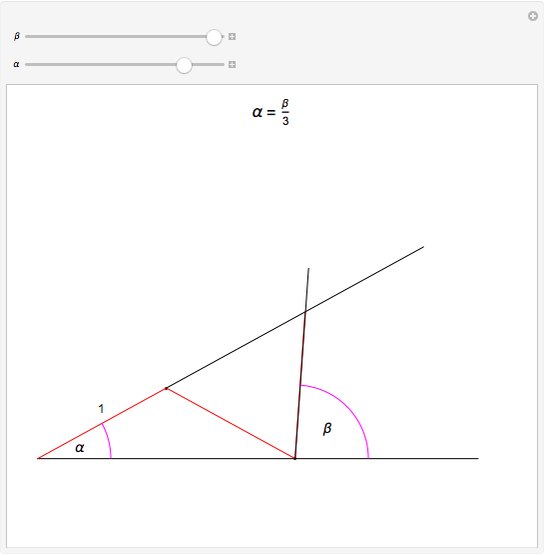
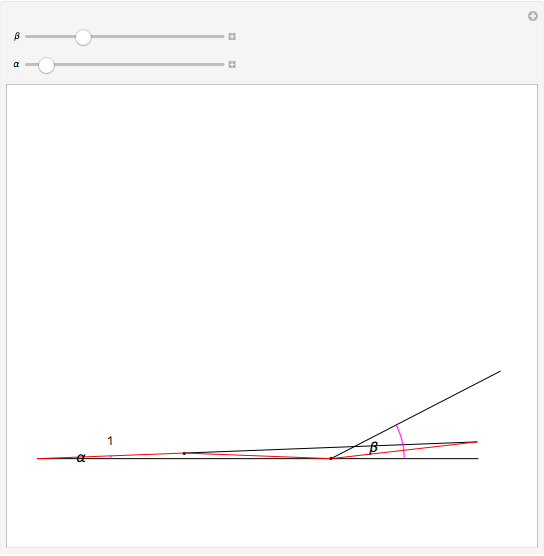
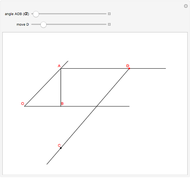
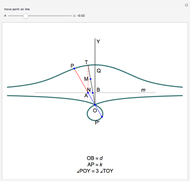
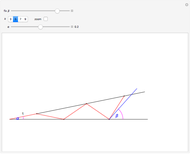
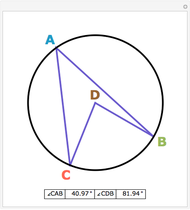
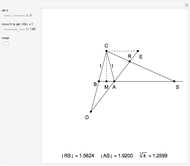
This Demonstration shows Pascal's angle trisection. The red segments are the same length. Vary so that the last red segment overlaps the top ray of angle . Then is one-third the size of .

Contributed by: Izidor Hafner (July 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

J. Bryant and C. Sangwin, How Round Is Your Circle?, Princeton, NJ: Princeton University Press, 2008 p. 107.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send