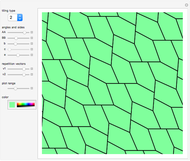
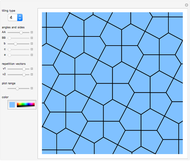
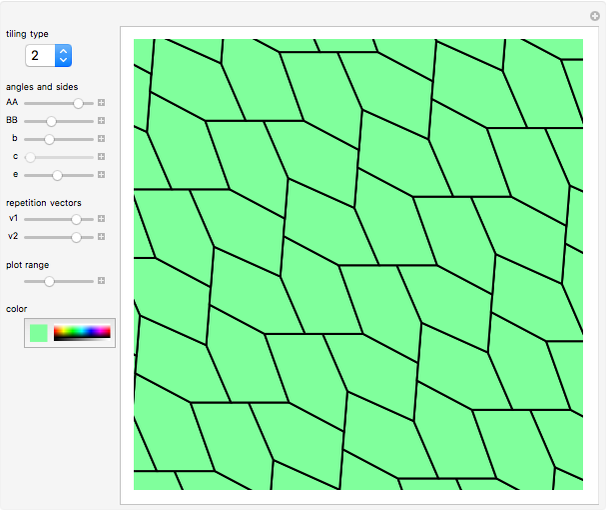
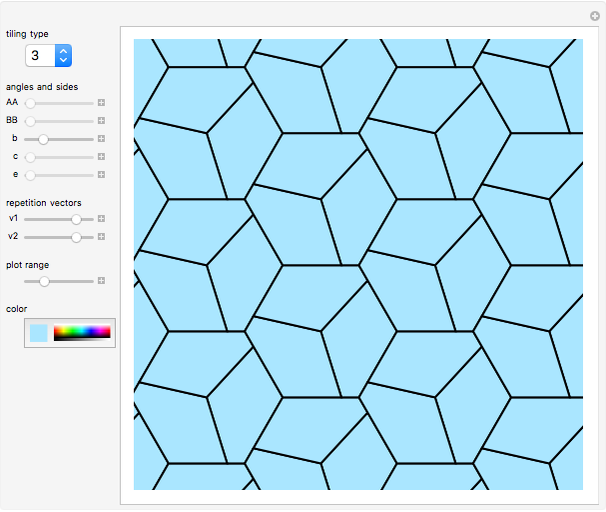
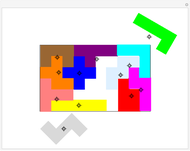
Pentagon Tilings

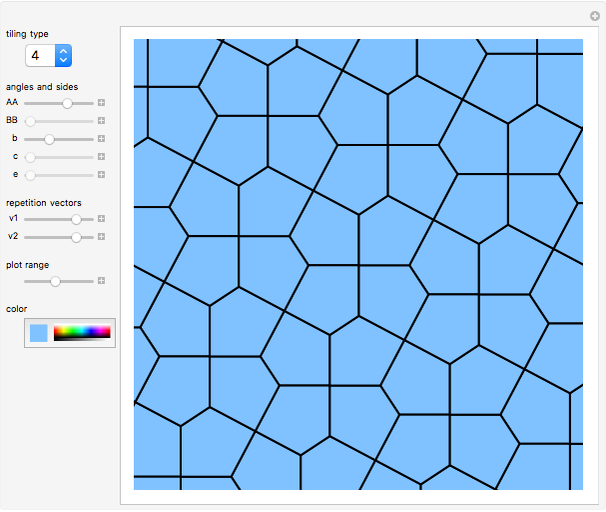
In 1918, K. Reinhardt discovered five different families of convex pentagons that could tile the plane (1-5). This was the complete list until 1968, when Richard Kershner wrote about three more families of tiling pentagons (6-8). Martin Gardner wrote about the complete list of eight tiling pentagons in 1975, and then got a message from Richard James III about another type (10). Martin updated the readers of Mathematical Games, but then got a message from a housewife with no mathematical training, Marjorie Rice, who found four more families of tiling pentagons (8, 11-13). In 1985, Rolf Stein found a convex pentagon that can tile the plane. This Demonstration gives exact solutions for all 14 families.