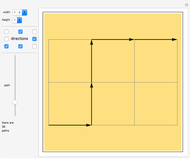
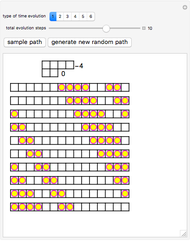
Periodic Box-Ball System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
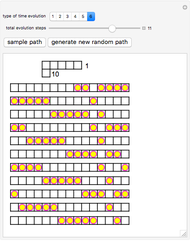
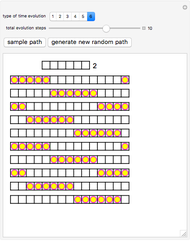
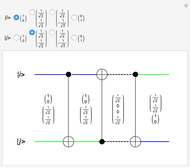
The periodic box-ball systems (PBBS for short) are typical examples of soliton cellular automata. Each group of balls constitutes a soliton; the groups exhibit nonlinear scattering with each other. PBBS are not only a limit of classical soliton systems but also a limit of quantum integrable models. In particular, the limit of various types of transfer matrices of quantum integrable models provides different types of time evolutions 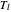 , where
, where 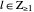 .
. 
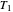 coincides with cyclic shift and the others form a commuting family of nontrivial time evolution operators that give integrability of the model. In this Demonstration, time evolutions proceed downwards. At the top is the rigged configuration, which is the action-angle variable (i.e., the constant of motion and the linearization parameter) corresponding to the bottom line.
coincides with cyclic shift and the others form a commuting family of nontrivial time evolution operators that give integrability of the model. In this Demonstration, time evolutions proceed downwards. At the top is the rigged configuration, which is the action-angle variable (i.e., the constant of motion and the linearization parameter) corresponding to the bottom line.
Contributed by: Reiho Sakamoto (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Box-ball systems (BBS for short) were introduced by Takahashi–Satsuma in 1990 in their study of the construction of examples of soliton cellular automata. The periodic version of BBS (PBBS) was then introduced by Yura–Tokihiro in 2001. Since then BBS were extensively studied because many deep and unexpected connections with different branches of mathematics and mathematical physics were discovered. Among those are connections with the theory of the crystal base of quantum affine algebras, various topics in combinatorics, the Riemann theta functions, tropical algebraic geometry, and the theory of discrete KP- and Toda-type integrable systems. For example, local time evolution rules of BBS and PBBS are identical to the combinatorial  -matrices of the crystal base theory.
-matrices of the crystal base theory.
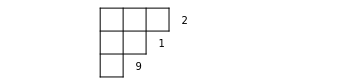
A recent breakthrough is the discovery of the connection with the rigged configurations (RC for short) that were originally discovered by Kerov–Kirillov–Reshetikhin in 1986 during their study of the Bethe ansatz of the quantum integrable models (Kuniba–Okado–Sakamoto–Takagi–Yamada 2006 for BBS and Kuniba–Takagi–Takenouchi 2006 for PBBS). RC are depicted by Young diagrams associated with integers. Roughly speaking, each row represents a soliton of the length equal to the row and integers determine the positions of such solitons. Similar machinery is established for a wider class of algebras and yields general solutions of BBS and PBBS. Note that in this Demonstration, the periodic boundary condition leads us to consider the quotient space of the set of RC.
Interested readers are invited to read the following research paper to get comprehensive information of known results and references related with this Demonstration: A. N. Kirillov and R. Sakamoto, "Relationships between Two Approaches: Rigged Configurations and 10-Eliminations," Letters in Mathematical Physics, 89, 2009 pp. 51–65.
Permanent Citation